
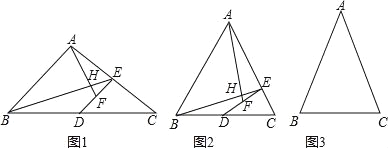
【题目】△ABC中,AB=AC,取BC的中点D,做DE⊥AC与点E,取DE的中点F,连接BE,AF交于点H.
(1)如图1,如果∠BAC=90°,那么∠AHB= °,![]() = ;
= ;
(2)如图2,如果∠BAC=60°,猜想∠AHB的度数和![]() 的值,并证明你的结论;
的值,并证明你的结论;
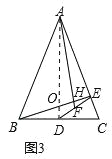
(3)如果∠BAC=α,那么![]() = .(用含α表达式表示)
= .(用含α表达式表示)
【答案】(1)90;![]() ;(2)90;
;(2)90;![]()
【解析】
试题分析:连接AD,根据等腰三角形的性质可得∠ABC=∠C,∠BAD=![]() ∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=
∠BAC,AD⊥BC,然后根据同角的余角相等可得∠ADE=∠C.易证△ADB∽△DEC,可得ADCE=BDDE.由此可得ADCE=![]() BC2DF=BCDF,即
BC2DF=BCDF,即![]() ,由此可证到△AFD∽△BEC,则有
,由此可证到△AFD∽△BEC,则有![]() .在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-
.在Rt△ADB中根据三角函数的定义可得tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,从而可得
,从而可得![]() =
=![]() tan(90°-
tan(90°-![]() ∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的三个问题.
∠BAC).由△AFD∽△BEC可得∠DAF=∠CBE,即可得到∠DAF+∠AOH=∠CBE+∠BOD=90°,即可得到∠AHB=90°.利用以上结论即可解决题中的三个问题.
试题解析:连接AD,

∵AB=AC,点D是BC的中点,
∴∠ABC=∠C,∠BAD=∠DAC=![]() ∠BAC,AD⊥BC,
∠BAC,AD⊥BC,
∵AD⊥BC,DE⊥AC,
∴∠ADE+∠CDE=90°,∠C+∠CDE=90°,
∴∠ADE=∠C.
又∵∠ADB=∠DEC=90°,
∴△ADB∽△DEC,
∴![]() ,即AD·CE=BD·DE.
,即AD·CE=BD·DE.
∵点D是BC的中点,点F是DE的中点,
∴BD=![]() BC,DE=2DF,
BC,DE=2DF,
∴ADCE═![]() BC2DF=BCDF,
BC2DF=BCDF,
∴![]() ,
,
又∵∠ADE=∠C,
∴△AFD∽△BEC,
∴![]() .
.
在Rt△ADB中,
∵∠ABD=90°-∠BAD=90°-![]() ∠BAC,BD=
∠BAC,BD=![]() BC,
BC,
∴tan∠ABD=tan(90°-![]() ∠BAC)=
∠BAC)=![]() ,
,
∴![]() tan(90°-
tan(90°-![]() ∠BAC).
∠BAC).
∵△AFD∽△BEC,∴∠DAF=∠CBE.
∵∠CBE+∠BOD=90°,∠AOH=∠BOD,
∴∠DAF+∠AOH=∠CBE+∠BOD=90°,
∴∠AHO=180°-90°=90°,即∠AHB=90°.
(1)如图1,
根据以上结论可得:
∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() ×90°)=
×90°)=![]() .
.
(2)如图2,

猜想:∠AHB=90°,![]() .
.
证明:根据以上结论可得:
∠AHB=90°,![]() =
=![]() tan(90°-
tan(90°-![]() ×60°)=
×60°)=![]() .
.
(3)如图3,
根据以上结论可得:
![]() =
=![]() tan(90°-
tan(90°-![]() α).
α).


科目:初中数学 来源: 题型:
【题目】某文具店去年8月底购进了一批文具1160件,预计在9月份进行试销.购进价格为每件10元.若售价为12元/件,则可全部售出.若每涨价0.1元.销售量就减少2件.
(1)求该文具店在9月份销售量不低于1100件,则售价应不高于多少元?
(2)由于销量好,10月份该文具进价比8月底的进价每件增加20%,该店主增加了进货量,并加强了宣传力度,结果10月份的销售量比9月份在(1)的条件下的最低销售量增加了m%,但售价比9月份在(1)的条件下的最高售价减少![]() m%.结果10月份利润达到3388元,求m的值(m>10).
m%.结果10月份利润达到3388元,求m的值(m>10).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列几何图形中,绕其对称中心点旋转任意角度后,所得到的图形都和原图形重合,这个图形是( )
A. 正方形 B. 正六边形 C. 五角星 D. 圆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
(1)a=b,∠A=45°
(2)∠A=32°,∠B=58°
(3)a=5,b=12,c=13
A. 1个B. 2个C. 3D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com