
【题目】已知:抛物线![]() 交x轴于A,B两点,交y轴于点C,其中点B在点A的右侧,且AB=7.
交x轴于A,B两点,交y轴于点C,其中点B在点A的右侧,且AB=7.
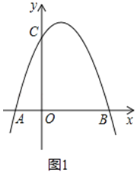
(1)如图1,求抛物线的解析式;
(2)如图2,点D在第一象限内抛物线上,连接CD,AD,AD交y轴于点E.设点D的横坐标为d,△CDE的面积为S,求S与d之间的函数关系式(不要求写出自变量d的取值范围);
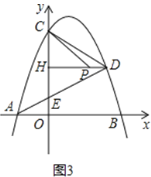
(3)如图3,在(2)的条件下,过点D作DH⊥CE于点H,点P在DH上,连接CP,若∠OCP=2∠DAB,且HE:CP=3:5,求点D的坐标及相应S的值.
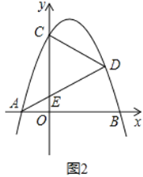
【答案】(1)![]() ;(2)
;(2)![]() ;(3)D(4,3),8
;(3)D(4,3),8
【解析】
(1)先求出点A,B的坐标,结合AB的长,即可得到答案;
(2)过点D作DK⊥x轴于点K,过点D作DH⊥CE于点H,设∠DAB=α,易得![]() ,进而求出CE的长,即可求解;
,进而求出CE的长,即可求解;
(3)过点E作CE的垂线,过C作∠OCP的平分线交DE于点J,交CE的垂线于点F,过点F作ED的平行线交HD的延长线于点N,连接CN.易得∠ECF=∠DAB=∠HDE=∠PCF=α,设HE=3k,CP=5k,先证△CFN为等腰三角形,再证PC=PN=5k,由勾股定理得(d﹣3k)2+(d﹣2k)2=(5k)2,可得![]() ,结合
,结合![]() ,即可求解.
,即可求解.
(1)∵![]() ,令y=0,则(x+2)(x﹣m)=0,解得:
,令y=0,则(x+2)(x﹣m)=0,解得:![]() ,
,
∴A(﹣2,0),B(m,0),
∵AB=7,
∴m﹣(﹣2)=7,m=5,
∴![]() ;
;
(2)过点D作DK⊥x轴于点K,过点D作DH⊥CE于点H,设∠DAB=α,
∵点D在第一象限内抛物线上,点D的横坐标为d,
∴![]() ,
,
∴ ,
,
∵C(0,5),
∴EO=AOtanα=5﹣d,CE=5﹣(5﹣d)=d,
∴![]() ;
;
(3)过点E作CE的垂线,过C作∠OCP的平分线交DE于点J,交CE的垂线于点F,过点F作ED的平行线交HD的延长线于点N,连接CN.
∵EF⊥CE,DH⊥CE,
∴EF∥DH∥AB,
∵设∠DAB=α,∠OCP=2∠DAB,CF平分∠OCP,
∴∠ECF=∠DAB=∠HDE=∠PCF=α,
∵HE:CP=3:5,
∴设HE=3k,CP=5k,
由(2)可知:CE=HD=d,
又∵∠CEF=∠CHD=90°,
∴△CEF≌△DHE(ASA),
∴EF=HE,CF=DE,
∵EF∥DN,NF∥DE,
∴四边形EDNF为平行四边形,
∴EF=HE=DN=3k,CF=DE=FN,∠DNF=∠DEF=α,
∴△CFN为等腰三角形,
∴∠FCN=∠FNC,
∴∠PCN=∠FCN-α=∠FNC-α=∠PNC,
∴PC=PN=5k,
∴PD=2k,
∴CH=d﹣3k,PH=d﹣2k,
∴(d﹣3k)2+(d﹣2k)2=(5k)2,
∴(d﹣6k)(d+k)=0,
∴d=6k,
∴在Rt△DHE中,![]() ,
,
由(2)知![]() ,
,
∴![]() .
.
∴d=4,
∴D(4,3),![]() .
.


科目:初中数学 来源: 题型:
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,与y轴交于点C,点D为顶点.
两点,与y轴交于点C,点D为顶点.
![]() 求抛物线解析式及点D的坐标;
求抛物线解析式及点D的坐标;
![]() 若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有
若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有![]() 且只有三个时,求直线l的解析式;
且只有三个时,求直线l的解析式;
![]() 如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到
如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 与抛物线的交点坐标.
与抛物线的交点坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
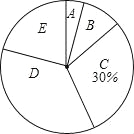
【题目】今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
(1)求全班学生人数和m的值.
(2)直接写出该班学生的中考体育成绩的中位数落在哪个分数段.
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
分组 | 分数段(分) | 频数 |
A | 36≤x<41 | 2 |
B | 41≤x<46 | 5 |
C | 46≤x<51 | 15 |
D | 51≤x<56 | m |
E | 56≤x<61 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
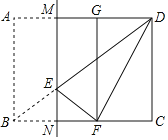
【题目】如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经销-种进价为每千克50元的水产品,据市场分析,每千克售价为60元时,月销售量为![]() ,销售单价每涨1元时,月销售量就减少
,销售单价每涨1元时,月销售量就减少![]() ,针对这种情况,请解答以下问题:
,针对这种情况,请解答以下问题:
(1)当销售单价定为65元时,计算销售量和月销售利润;
(2)若想在月销售成本不超过12000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,连结
,连结![]() ,且
,且![]() 平分
平分![]() .
.
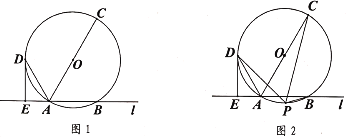
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)如图2,在(2)的条件下,点![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,
,![]() ,问:线段
,问:线段![]() ,
,![]() ,
,![]() 之间存在什么数量关系?请说明理由.
之间存在什么数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
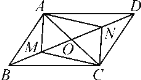
【题目】如图,在ABCD中,M,N是BD上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是菱形,这个条件是( )
A.OM=![]() ACB.MB=MO
ACB.MB=MO
C.BD⊥ACD.∠AMB=∠CND
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com