
【题目】如图,动点![]() 在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点
在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点![]() ,第2次运动到点
,第2次运动到点![]() ,第3次运动到点
,第3次运动到点![]() ,.….按照这样的运动规律,点
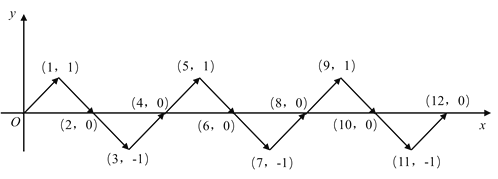
,.….按照这样的运动规律,点![]() 第17次运动到点( )
第17次运动到点( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
令P点第n次运动到的点为Pn点(n为自然数).列出部分Pn点的坐标,根据点的坐标变化找出规律“P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1)”,根据该规律即可得出结论.
令P点第n次运动到的点为Pn点(n为自然数).
观察,发现规律:P0(0,0),P1(1,1),P2(2,0),P3(3,-1),P4(4,0),P5(5,1),…,
∴P4n(4n,0),P4n+1(4n+1,1),P4n+2(4n+2,0),P4n+3(4n+3,-1).
∵17=4×4+1,
∴P第17次运动到点(17,1).
故选:A.


科目:初中数学 来源: 题型:
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)
 根据表、图提供的信息,解决以下问题:
根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;

(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
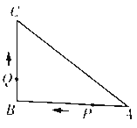
【题目】如图,已知△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q是△ABC边上的两个动点,点P从点A开始沿A→B方向运动,且速度为1 cm,点Q从点B开始沿B→C方向运动,且速度为2 cm/s,它们同时出发,设运动的时间为t s.
(1)运动几秒时,△APC是等腰三角形?
(2)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:当![]() ,
,![]() 时,∵
时,∵![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号.请利用上述结论解决以下问题:
时取等号.请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为_______;当
的最小值为_______;当![]() 时,
时,![]() 的最大值为__________.
的最大值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
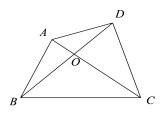
(3)如图,四边形ABCD的对角线AC ,BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D,且AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
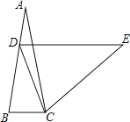
A. 80° B. 70° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地之间有一条直线跑道,甲,乙两人分别从
两地之间有一条直线跑道,甲,乙两人分别从![]() 、
、![]() 同时出发,相向而行均速跑步,且乙的速度是甲速度的80%,当甲,乙两人分别到达
同时出发,相向而行均速跑步,且乙的速度是甲速度的80%,当甲,乙两人分别到达![]() 地,
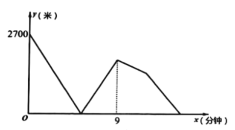
地,![]() 地后立即掉头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行).甲,乙两人之间的距离
地后立即掉头往回跑,甲的速度保持不变,乙的速度提高25%(仍保持匀速前行).甲,乙两人之间的距离![]() (米)与跑步时间
(米)与跑步时间![]() (分钟)之间的关系如图所示,则他们在第二次相遇时距
(分钟)之间的关系如图所示,则他们在第二次相遇时距![]() 地___________米.
地___________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:对于平面直角坐标系中的任意两点![]() ,
,![]() ,我们把
,我们把![]() 叫做
叫做![]() ,
,![]() 两点间的距离公式,记作
两点间的距离公式,记作![]() ,如:
,如:![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为
两点的距离为![]()
请根据以上的阅读材料,解答下列问题:
(1)当![]() ,
,![]() 的距离
的距离![]() ,求出
,求出![]() 的值.
的值.
(2)若在平面内有一点![]() ,使
,使![]() 有最小值,求出它最小值和此时
有最小值,求出它最小值和此时![]() 的范围.
的范围.
(3)若![]() 有最小值,请直接写出最小值.
有最小值,请直接写出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
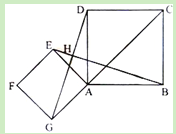
【题目】如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)求证:EB=GD;
(2)判断EB与GD的位置关系,并说明理由;
(3)若AB=2,AG=![]() ,求EB的长.
,求EB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com