
【题目】在平面直角坐标系xOy中,已知点B(8,0)和点C(9, ![]() ).抛物线
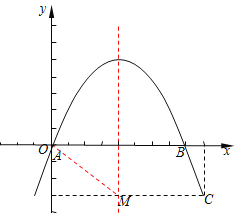
).抛物线![]() (a,c是常数,a≠0)经过点B、C,且与x轴的另一交点为A.对称轴上有一点M ,满足MA=MC.
(a,c是常数,a≠0)经过点B、C,且与x轴的另一交点为A.对称轴上有一点M ,满足MA=MC.
(1)求这条抛物线的表达式;
(2)求四边形ABCM的面积;
(3)如果坐标系内有一点D,满足四边形ABCD是等腰梯形,且AD//BC,求点D的坐标.
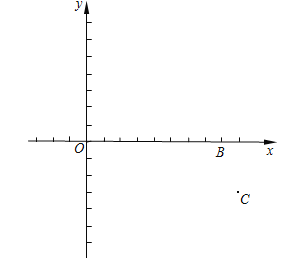
【答案】(1)![]() ;(2)
;(2)![]() ;(3)(
;(3)(![]() ,
, ![]() )
)
【解析】试题分析:(1)根据抛物线的解析式,求得抛物线的对称轴,根据抛物线的对称性求得点A的坐标,再将A、C的坐标代入函数解析式,求得a、c的值,即可求得这条抛物线的表达式;(2)因点M在对称轴上,设M(4,y),由MA=MC,即![]() ,根据勾股定理列出方程
,根据勾股定理列出方程![]() ,解得y=-3,即可得M(4,-3),再由四边形ABCM为梯形,根据梯形的面积公式即可求得四边形ABCM的面积;(3)用待定系数法求得直线BC的解析式,因AD//BC,即可求得直线AD的解析式,设D(x,-3x),根据勾股定理得方程
,解得y=-3,即可得M(4,-3),再由四边形ABCM为梯形,根据梯形的面积公式即可求得四边形ABCM的面积;(3)用待定系数法求得直线BC的解析式,因AD//BC,即可求得直线AD的解析式,设D(x,-3x),根据勾股定理得方程![]() 解得x的值,即可求得点D的坐标.
解得x的值,即可求得点D的坐标.
试题解析:
(1)由题意得:抛物线对称轴![]() ,即
,即![]() .
.
点B(8,0)关于对称轴的对称点为点A(0,0)∴![]() ,将C(9,-3)代入
,将C(9,-3)代入![]() ,得
,得![]()
∴抛物线的表达式:![]()
(2)∵点M在对称轴上,∴可设M(4,y)
又∵MA=MC,即![]()
∴![]() ,解得y=-3,∴M(4,-3)
,解得y=-3,∴M(4,-3)
∵MC//AB且MC≠AB,∴四边形ABCM为梯形,,AB=8,MC=5,AB边上的高h=yM=3
∴![]()
(3)将点B(8,0)和点C(9,﹣3)代入![]() 可得
可得
![]() ,解得
,解得![]()
由题意得.∵AD//BC,![]() ∴
∴![]() ,
,![]()
又∵AD过(0,0),DC=AB=8,设D(x,-3x),
![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴![]() ,
,
∴点D的坐标![]() .
.


科目:初中数学 来源: 题型:
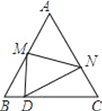
【题目】如图,等边△ABC中,D是边BC上的一点,且BD:DC=3:5,把△ABC折叠,使点A落在边BC上的点D处,若AM=5,那么AN的长度为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二青会开幕式期间,出租车司机李师傅营运时是在南北走向的滨河西路上行进的,如果规定向南为正,向北为负,他这天上午所接![]() 位乘客的行车里程(单位:
位乘客的行车里程(单位:![]() )为:
)为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(假设相邻两位乘客上下车没有时间间隔)
.(假设相邻两位乘客上下车没有时间间隔)
(1)试判断李师傅将最后一位乘客送到目的地时,他在出发点的什么方向,距离出发地多少千米?
(2)若汽车耗油量为![]() ,则这天上午李师傅接送乘客时出租车共耗油多少升?
,则这天上午李师傅接送乘客时出租车共耗油多少升?
(3)若出租车起步价为![]() 元,起步里程为
元,起步里程为![]() (包括
(包括![]() ),超过部分每千米
),超过部分每千米![]() 元,问李师傅这天上午共得车费多少元?
元,问李师傅这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB,请按要求完成下列问题.
(1)用直尺和圆规作图,延长线段AB到点C,使BC=AB;反向延长线段AB到点D,使AD=AC;
(2)如果AB=2cm;
①求CD的长度;
②设点P是线段BD的中点,求线段CP的长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张分别标有数字2,3,4,6的扑克牌,除正面的数字外,牌的形状、大小完全相同.小红先从口袋中随机摸出一张扑克牌并记下牌上的数字为x;小颖在剩下的3张扑克牌中随机摸出一张扑克牌并记下牌上的数字为y,
(1)事件①:小红摸出标有数字3的牌,事件②:小颖摸出标有数字1的牌,则( )
A.事件①是必然事件,事件②是不可能事件,
B.事件①是随机事件,事件②是不可能事件,
C.事件①是必然事件,事件②是随机事件,
D.事件①是随机事件,事件②是必然事件,
(2)若|x-y|≤2,则说明小红与小颖“心领神会”,请求出她们“心领神会”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上,点A和点B分别位于原点O两侧,AB=14,点A对应的数为a,点B对应的数为b.
(1) 若b=-4,则a的值为__________.
(2) 若OA=3OB,求a的值.
(3) 点C为数轴上一点,对应的数为c.若O为AC的中点,OB=3BC,直接写出所有满足条件的c的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com