
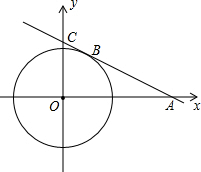
 如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,且半径为1的⊙O有公共点B,问:
如图,直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,且半径为1的⊙O有公共点B,问:分析 (1)作OD⊥AC于D,则∠ODA=90°,由直线解析式得出A(2,0),C(0,$\frac{2\sqrt{3}}{3}$),得出OA=2,OC=$\frac{2\sqrt{3}}{3}$,由三角函数求出∠A=30°,由含30°角的直角三角形的性质得出OD=$\frac{1}{2}$OA=1,即可得出直线AC与⊙O相切;
(2)由直线与⊙O有公共点B,得出B为切点与D重合,即可得出AB=$\sqrt{3}$OD=$\sqrt{3}$.
解答 解:(1)直线AC与⊙O相切,理由如下: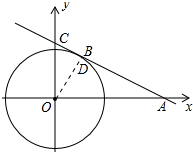
作OD⊥AC于D,则∠ODA=90°,
∵直线y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$交坐标轴于A、C两点,
∴A(2,0),C(0,$\frac{2\sqrt{3}}{3}$),
∴OA=2,OC=$\frac{2\sqrt{3}}{3}$,
∴tan∠OAC=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∴OD=$\frac{1}{2}$OA=1,
∴直线AC与⊙O相切;
(2)由(1)得:直线AC与⊙O相切,
∵直线与⊙O有公共点B,
∴B为切点与D重合,
∴AB=$\sqrt{3}$OD=$\sqrt{3}$.
点评 本题考查了直线与圆的位置关系的判定方法、一次函数图象上点的坐标特征、三角函数、含30°角的直角三角形的性质等知识;本题综合性强,有一定难度,证明直线与圆相切是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
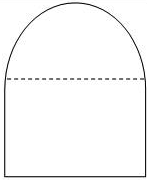 如图,是某一城市地铁的横截面,上面为半圆形,下面为矩形,矩形的长和宽分别为a m与b m.
如图,是某一城市地铁的横截面,上面为半圆形,下面为矩形,矩形的长和宽分别为a m与b m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第 一 档 | 第 二 档 | 第 三 档 | 第 四 档 | |
| 凳高(cm) | 38 | 40 | 42 | 44 |
| 桌高(cm) | 70(76-6) | 74(80-6) | 78(84-6) | 82(88-6) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com