
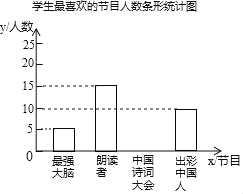
【题目】为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如图统计图表:根据以上提供的信息,解答下列问题:
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
(1)x= ,a= ,b= ;
(2)补全上面的条形统计图;
(3)在喜爱《最强大脑》的学生中,有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动,请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
【答案】(1)50;20;30;(2)见解析;(3)![]() ;
;
【解析】
(1)根据最强大脑的人数除以占的百分比确定出x的值,进而求出a与b的值即可;
(2)根据a的值,补全条形统计图即可;
(3)列出所有情况,即可看出所抽取的2名同学恰好是1名男同学和1名女同学的情况,再用此情况数量除以所有情况数量即可.
(1)根据题意得:x=5÷10%=50,a=50×40%=20,b=![]() ×100=30;
×100=30;
故答案为:50;20;30;
(2)中国诗词大会的人数为20人,补全条形统计图,如图所示:

(3)∵5﹣2=3(名),
∴喜爱最强大脑的5名同学中,有3名男同学,2名女同学,
男1 | 男2 | 男3 | 女1 | 女2 | |
男1 | ﹣﹣﹣ | 男2,男1 | 男3,男1 | 女1,男1 | 女2,男1 |
男2 | 男1,男2 | ﹣﹣﹣ | 男3,男2 | 女1,男2 | 女2,男2 |
男3 | 男1,男3 | 男2,男3 | ﹣﹣﹣ | 女1,男3 | 女2,男3 |
女1 | 男1,女1 | 男2,女1 | 男3,女1 | ﹣﹣﹣ | 女2,女1 |
女2 | 男1,女2 | 男2,女2 | 男3,女2 | 女1,女2 | ﹣﹣﹣ |
所有等可能的情况有20种,其中抽取的2名同学恰好是1名男同学和1名女同学的情况有12种,
则P(一男一女)=![]() =
=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,等腰Rt△ABC,等腰Rt△ADE,AB⊥AC,AD⊥AE,AB=AC,AD=AE,CD交AE、BE分别于点M、F
(1)求证:△DAC≌△EAB;
(2)若∠AEF=15°,EF=4,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
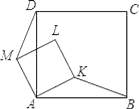
【题目】如图,K是正方形ABCD内一点,以AK为一边作正方形AKLM,使L,M,D在AK的同旁,连接BK和DM,试用旋转的思想说明线段BK与DM的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,把矩形COAB绕点C顺时针旋转α角,得到矩形CFED.设FC与AB交于点H,且A(0,4),C(8,0).
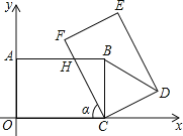
(1)当α=60°时,△CBD的形状是______;
(2)设AH=m
①连接HD,当△CHD的面积等于10时,求m的值;
②当0°<α<90°旋转过程中,连接OH,当△OHC为等腰三角形时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
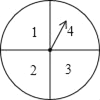
【题目】小王和小张利用如图所示的转盘做游戏,转盘的盘面被分为面积相等的4个扇形区域,且分别标有数字1,2,3,4.游戏规则如下:两人各转动转盘一次,分别记录指针停止时所对应的数字,如两次的数字都是奇数,则小王胜;如两次的数字都是偶数,则小张胜;如两次的数字是奇偶,则为平局.解答下列问题:
(1)小王转动转盘,当转盘指针停止,对应盘面数字为奇数的概率是多少?
(2)该游戏是否公平?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①是一个重要公式的几何解释.请你写出这个公式;
(2)如图②,Rt△ABC≌Rt△CDE,∠B=∠D=90°,且B、C、D三点在一条直线上.试证明∠ACE=90°;
(3)伽菲尔德(G a rfield,1881年任美国第20届总统)利用(1)中的公式和图②证明了勾股定理(1876年4月1日,发表在《新英格兰教育日志》上),现请你尝试该证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市计划购进甲、乙两种商品,甲种商品的进价比乙种商品的进价每件多80元,若用720元购进甲种商品的件数与用360元购进乙种商品的件数相同.
(1)求甲、乙两种商品的进价各是多少元?
(2)已知甲种商品的售价为240元/件,乙种商品的售价为130元/件,若超市销售甲、乙两种商品共80件,其中销售甲种商品为![]() 件(
件(![]() ),设销售完80件甲、乙两种商品的总利润为
),设销售完80件甲、乙两种商品的总利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式,并求出
之间的函数关系式,并求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.
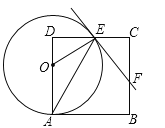
(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=∠C,点D在AC上,点E在BC上,AD=CE,BC=DC
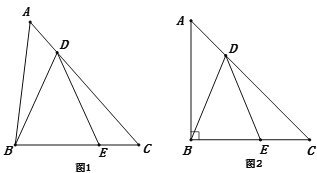
(1)求证:DB=DE;
(2)如图2,若∠ABC=90°,求∠BED的度数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com