
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=ABAD;
(2)若AD=4,AB=6,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)由AC平分∠DAB,∠ADC=∠ACB=90°,可证得△ADC∽△ACB,然后由相似三角形的对应边成比例,证得AC2=ABAD;
(2)易证得△AFD∽△CFE,然后由相似三角形的对应边成比例,求得![]() 的值.
的值.
试题解析:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=ABAD;
(2)∵∠ACB=90°,E为AB中点,
∴AE=CE,
∴∠CAE=∠ECA,
∵AC平分∠DAB,
∴∠DAC=∠EAC,
∴∠DAC=∠ACE,
∴CE∥AD,
∴△AFD∽△CFE,
∴AD:CE=AF:CF,
∵CE=![]() AB,
AB,
∴CE=![]() ×6=3,
×6=3,
∵AD=4,
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将边长为1的小正方形拼成一行一字排开,A1、A2、A3…依次是第2、3、4…个小正方形右下角的顶点,P是第一个小正方形左上角的顶点.记△PA1A2、△PA1A3,△PA1A4…依次为①号三角形、②号三角形、③号三角形….已知这些三角形中有一个三角形与①号三角形相似,则这个三角形的号数为( )

A. ③ B. ④ C. ⑤ D. ⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示为一个无盖的正方体纸盒,现将其展开成平面图,如图(2)所示.已知展开图中每个正方形的边长为1:
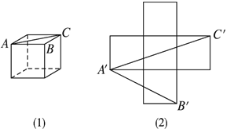
(1)在展开图(2)中可画出最长线段的长度为 ,在平面展开图(2)中这样的最长线段一共能画出 条。
(2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,已知∠C=90°,sinB=![]() ,AC=8,D为线段BC上一点,CD=2.
,AC=8,D为线段BC上一点,CD=2.
(1)求BD的值;
(2)求cos∠DAC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车行驶时的耗油量为0.1升/千米,如图是油箱剩余油量![]() (升)关于加满油后已行驶的路程
(升)关于加满油后已行驶的路程![]() (千米)的函数图象.
(千米)的函数图象.

(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量;
(2)求![]() 关于
关于![]() 的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲乙两个不透明的布袋,甲布袋装有2个形状和重量完全相同的小球,分别标有数字1和2;乙布袋装有3个形状和重量完全相同的小球,分别标有数字﹣3,﹣1和0.先从甲布袋中随机取出一个小球,将小球上标有的数字记作x;再从乙布袋中随机取出一个小球,再将小球标有的数字记作y.
(1)用画树状图或列表法写出两次摸球的数字可能出现的所有结果;
(2)若从甲、乙两布袋中取出的小球上面的数记作点的坐标(x,y),求点(x,y)在一次函数y=﹣2x+1图象上的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015镇江)
活动1:在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
活动2:在一只不透明的口袋中装有标号为1,2,3,4的4个小球,这些球除标号外都相同,充分搅匀,请你对甲、乙、丙三名同学规定一个摸球顺序: → → ,他们按这个顺序从袋中各摸出一个球(不放回),摸到1号球胜出,则第一个摸球的同学胜出的概率等于 ,最后一个摸球的同学胜出的概率等于 .
猜想:在一只不透明的口袋中装有标号为1,2,3,…,n(n为正整数)的n个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:这三名同学每人胜出的概率之间的大小关系.
你还能得到什么活动经验?(写出一个即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com