
【题目】如图,点E,F分别是正方形ABCD内部、外部的点,四边形ADFE与四边形BCFE均为菱形,连接AF,BF.有如下四个结论:①![]() ;②
;②![]() ;③EF垂直平分DC;④
;③EF垂直平分DC;④![]() ;其中正确的是( )
;其中正确的是( )
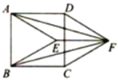
A.①②④B.①②③C.①③④D.①③
【答案】D
【解析】
根据菱形和正方形的性质,即可得到![]() ;由△DCF是等边三角形,得到∠FDC=60°,则
;由△DCF是等边三角形,得到∠FDC=60°,则![]() ;由△CDF是等边三角形,AD⊥CD,AD∥EF,即可得到EF垂直平分DC;延长FE,交AB于点G,则
;由△CDF是等边三角形,AD⊥CD,AD∥EF,即可得到EF垂直平分DC;延长FE,交AB于点G,则![]() ,
,![]() ,由
,由![]() ,即可判断.
,即可判断.
解:根据题意,在正方形ABCD,菱形ADFE,菱形BCFE中,
∴![]() ,故①正确;
,故①正确;
∵![]() ,
,
∴△ABE是等边三角形,△DCF是等边三角形,
∴∠AEB=60°,∠FDC=60°
∴∠ADF=90°+60°=150°,
∴![]() ,故②错误;
,故②错误;
∵AD⊥CD,AD∥EF,
∴EF⊥CD,
∵△DCF是等边三角形,
∴EF垂直平分DC;故③正确;
延长FE,交AB于点G,
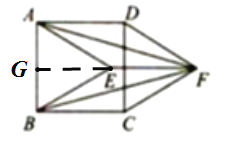
∵EF⊥CD,AB∥CD,
∴EF⊥AB,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,故④错误;
,故④错误;
∴正确的结论有:①③.
故选择:D.


科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
如:P(1,4)的“2属派生点为P′(1+2×4,2×1+4),即P′(9,6);
(1)点P(-1,3)的“2属派生点”P′的坐标为______;
(2)若点P的“3属派生点”P′的坐标为(-1,3),则点P的坐标为______.
(3)若点P在x轴的正半轴上,点P的“k属派生点”为点P′,线段PP′的长度等于线段OP的长度,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
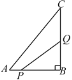
【题目】如图,在△ABC中,∠B=90°,AB=6 cm,BC=8 cm,若点P从点A沿AB边向B点以1 cm/s的速度移动,点Q从B点沿BC边向点C以2 cm/s的速度移动,两点同时出发.
(1)问几秒后,△PBQ的面积为8cm?
(2)出发几秒后,线段PQ的长为4![]() cm ?
cm ?
(3)△PBQ的面积能否为10 cm2?若能,求出时间;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
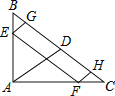
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=2,AC=3,D为BC的中点,动点E,F分别在AB,AC上,分别过点EG∥AD∥FH,交BC于点G、H,若EF∥BC,则EF+EG+FH的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导积极健康的生活方式、丰富居民生活,区推出系列文化活动,其中的乒乓球比赛采用单循环赛制(即每两名参赛者之间都要进行一场比赛)经统计,此次乒乓球比赛男子组共要进行28场单打.
(1)参加此次乒乓球男子单打比赛的选手有多少名?
(2)在系列文化活动中,社区与某旅行社合作组织“丰收节”采摘活动收费标准是:如果人数不超过20人,每人收费200元;如果超过20人,每增加1人,每人费用都减少5元经统计,社区共支付“采摘活动”费用4500元求参加此次“丰收节”采摘的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
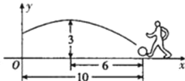
(1)如图建立直角坐标系,当球飞行的路线为一抛物线时,求此抛物线的解析式.
(2)已知球门高为2.44米,问此球能否射中球门(不计其它情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)化简函数解析式,当![]() 时,
时,![]() ___________,当
___________,当![]() 时
时![]() ____________;
____________;
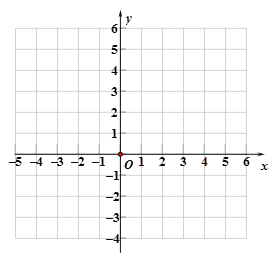
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;备用图
的图象;备用图
(3)结合画出的函数图象,解决问题:若关于![]() 的方程
的方程![]() 只有一个实数根,直接写出实数
只有一个实数根,直接写出实数![]() 的取值范围:___________________________.
的取值范围:___________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com