
【题目】如图,平行四边形ABCD中,E、F分别是边AD,BC的中点.张老师请同学们将纸条的下半部分即平行四边形ABFE沿EF翻折,得到一个V字形图案.
(1)请你在原图中画出翻折后的图形平行四边形A′B′FE(用尺规作图,不写画法,保留作图痕迹)
(2)已知∠A=63°,求∠B′FC的大小.

【答案】(1)图形见解析(2)54°
【解析】试题分析:(1)作∠NFE=∠BFE,∠MEK=∠AEK,然后在EM上截取A′E=AE,在NF上截取B′F=BF,连接A′B′,所得四边形A′B′FE即为所求;
(2)由平行四边形纸条ABCD中,E、F分别为AD、BC的中点,根据平行线分线段成比例定理,可得EF∥AB∥CD,即可求得∠B的度数,又由折叠的性质,即可得∠A=∠B′FE,又由∠B′FC=∠CFE-∠B′FE,即可求得∠B′FC的大小.
试题解析:(1)如图:

(2)∵平行四边形纸条ABCD中,E、F分别为AD、BC的中点,
∴EF∥AB∥CD,
∴∠B=∠CFE=180°﹣∠A=180°﹣63°=117°,
∵平行四边形ABEF沿EF翻折,得到翻折后的平行四边形A′B′FE,
∴∠A=∠B′FE=63°,
∴∠B′FC=∠CFE﹣∠B′FE=117°﹣63°=54°.


科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,点A,点C在直线a上.
(1)作△ABC关于直线a的轴对称图形△ADC;
(2)若∠BAC=35°,则∠BDA= ;
(3)△ABD的面积等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O, ∠AOM=90°,

(1)如图1,若OC平分∠AOM.求∠AOD的度数;
(2)如图2,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是长方形纸带,将纸带沿折叠成图2,再沿即折叠成图3,若在图1中∠DEF=a,则图3中∠CFE用含有a的式子表示=_______(0<a<60°) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答问题:
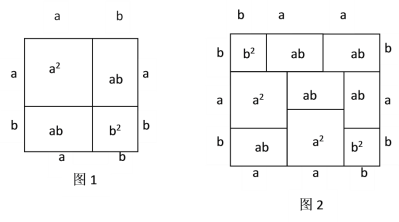
七年级第一学期课本中有这样一个思考题:“你能根据图1中的图形来说明完全平方公式吗?”说明如下:
图1中的面积可以表示为![]() ;图1中的面积又可以表示为
;图1中的面积又可以表示为![]() ;所以这个图形说明了完全平方公式
;所以这个图形说明了完全平方公式![]() 除了完全平方公式可以用图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.
除了完全平方公式可以用图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.
(1)请写出图2所表示的代数恒等式:__________________________________;
(2)请画一个图形,使它的面积能表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,已知三角形ABC,按要求画图:
(1)把三角形ABC向下平移4个小格,得到三角形A1B1C1,画出三角形A1B1C1.
(2)把三角形A1B1C1向右平移3个小格,得到三角形A2B2C2,画出三角形A2B2C2.
(3)经过2次平移,点P(x,y)的对应点P2的坐标是___________.
(4)三角形ABC的面积是___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”
,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角” ![]() 约为
约为![]() ,而当手指接触键盘时,肘部形成的“手肘角”
,而当手指接触键盘时,肘部形成的“手肘角”![]() 约为
约为![]() .图
.图![]() 是其侧面简化示意图,其中视线
是其侧面简化示意图,其中视线![]() 水平,且与屏幕
水平,且与屏幕![]() 垂直.
垂直.

(![]() )若屏幕上下宽
)若屏幕上下宽![]() ,科学使用电脑时,求眼睛与屏幕的最短距离
,科学使用电脑时,求眼睛与屏幕的最短距离![]() 的长.
的长.
(![]() )若肩膀到水平地面的距离
)若肩膀到水平地面的距离![]() ,上臂
,上臂![]() ,下臂
,下臂![]() 水平放置在键盘上,其到地面的距离
水平放置在键盘上,其到地面的距离![]() ,请判断此时
,请判断此时![]() 是否符合科学要求的
是否符合科学要求的![]() ?
?
(参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com