
【题目】如图,二次函数y=ax2+bx+2(a≠0)的图象与x 轴交于A,B 两点,与y 轴交于点C,已知点 A(-4,0),B(1,0).
(1)求抛物线的解析式;
(2)若点 D(m,n) 是抛物线在第二象限的部分上的一动点,四边形 ![]() 的面积为
的面积为 ![]() ,求
,求 ![]() 关于 m 的函数关系;
关于 m 的函数关系;
(3)若点 E 为抛物线对称轴上任意一点,当以 A,C,E 为顶点的三角形是直角三角形时,请求出满足条件的所有点 E 的坐标.

【答案】(1)![]()
(2) ![]()
(3) 
【解析】试题解析:(1)用待定系数法求出函数解析式即可;(2)用m表示出点D的坐标,过点D作DH⊥x轴于点H,利用四边形OCDA的面积=△ADH的面积+ 四边形OCDH的面积即可求得S关于 m 的函数关系;(3)求出函数的对称轴,设出点E的坐标,分∠AEC=90°、
∠ACE=90°和∠CAE=90°三种情况求点E的坐标即可.
试题分析:
(1)∵A(-4,0),B(1,0) 在二次函数y=ax2+bx+2(a≠0)的图象上,
∴![]() , 解得
, 解得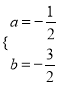 .
.
∴抛物线的解析式为![]() .
.
(2)∵ 点D(m,n)是抛物线在第二象限的部分上的一动点,
∴D(m, ![]() ),
),
过点D作DH⊥x轴于点H,
则DH=![]() ,AH=m+4,HO=-m,
,AH=m+4,HO=-m,
∵ 四边形OCDA的面积=△ADH的面积+ 四边形OCDH的面积,
∴![]() ,
,
化简,得![]() .
.
(3) 抛物线![]() 的对称轴为
的对称轴为![]() ,
,
故设点E的坐标为(![]() ).
).
∴![]() .
.
若∠AEC=90°,则![]() ,
,
解得![]() ,
,
此时点E的坐标是 或
或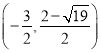 ;
;
若∠ACE=90°,则![]() ,
,
解得n=5,此时点E的坐标是![]() ;
;
若∠CAE=90°,则![]() ,
,
解得 n=-5,此时点E的坐标是![]() ;
;
综上所述点E的坐标是 或
或 或
或![]() 或
或![]() .
.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,A、B、C、D 为矩形的四个顶点,AB=16cm,AD=
6cm,动点P、Q 分别从A、C 同时出发,点P 以3cm/s的速度向点B 移动,
一直到达点 B 为止,点 Q 以2cm/s的速度向点 D 移动.
(1)P、Q 两点从出发点出发几秒时,四边形PBCQ 的面积是33cm2?
(2)P、Q 两点从出发点出发几秒时,点P、Q 间的距离是10cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
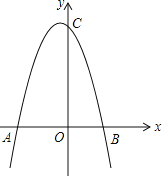
【题目】如图,抛物线y=﹣x2﹣x+6与x轴交于A、B两点,与y轴交于点C.
(1)求点A、B的坐标;
(2)设点P是线段AC上一点,且S△ABP:S△BCP=1:3,求点P的坐标;
(3)若直线y=![]() x+a与抛物线交于M、N两点,当∠MON为锐角时,求a的取值范围.
x+a与抛物线交于M、N两点,当∠MON为锐角时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 ![]() 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积为249900m2,请将249900精确到万位,并用科学记数法表示为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com