
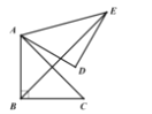
【题目】如图,在Rt△ABC中,∠ABC=90,AB=BC=![]() ,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,求BE的长为( )
,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,求BE的长为( )
A. 2+![]() B. 2
B. 2![]() C. 2+2
C. 2+2![]() D. 2
D. 2 ![]()
【答案】A
【解析】
首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后根据勾股定理求解.
由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,设BE与AC相交于点F,如下图所示,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在△ABF中,∠BFA=180°﹣45°﹣45°=90°可得∠AFB=∠AFE=90°在Rt△ABF中,由勾股定理得,BF=AF= =2,又在Rt△AFE中,∠AEF=30,°∠AFE=90°,FE=
=2,又在Rt△AFE中,∠AEF=30,°∠AFE=90°,FE= ![]() AF=2
AF=2![]() ,BE=BF+FE=2+2
,BE=BF+FE=2+2![]() .
.

故选:A


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】下列说法中,正确的有( )
(1)、![]() 的平方根是±5;(2)、五边形的内角和是540°;(3)、抛物线y=x2+2x+4与x轴无交点;(4)、等腰三角形两边长为6cm和4cm,则它的周长是16cm.
的平方根是±5;(2)、五边形的内角和是540°;(3)、抛物线y=x2+2x+4与x轴无交点;(4)、等腰三角形两边长为6cm和4cm,则它的周长是16cm.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
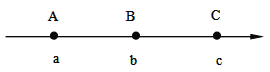
【题目】如图,数轴上的A,B,C三点所表示的数分别为a,b,c,其中AB=BC.如果![]() ,那么该数轴的原点O的位置应该在( )
,那么该数轴的原点O的位置应该在( )
A.点A的左边
B.点A与点B之间
C.点B与点C之间(靠近点B)
D.点C的右边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序如下:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试.两个程序的结果统计如下:

测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
查看答案和解析>>
科目:初中数学 来源: 题型:
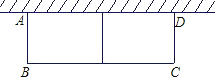
【题目】如图所示,某农户想建造一花圃,用来种植两种不同的花卉,以供应城镇市场需要,现用长为36m的篱笆,一面砌墙(墙的最大可使用长度l=13m),围成中间隔有一道篱笆的长方形花圃,设花圃宽AB为x,面积为S.
(1)求S与x的函数关系式.并指出它是一次函数,还是二次函数?
(2)若要围成面积为96m2的花圃,求宽AB的长度.
(3)花圃的面积能达到108m2吗?若能,请求出AB的长度,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市近期公布的居民用天然气阶梯价格听证会方案如下:
第一档天然气用量 | 第二档天然气用量 | 第三档天然气用量 |
年用天然气量 | 年用天然气量超出 | 年用天然气量 |
例:若某户![]() 年使用天气然
年使用天气然![]() 立方米,按该方案计算,则需缴纳天然气费为:
立方米,按该方案计算,则需缴纳天然气费为:![]() ×
×![]() +
+![]() ×(
×(![]() -
-![]() )=
)=![]() (元);依此方案请回答:
(元);依此方案请回答:
![]() 若小明家
若小明家![]() 年使用天然气
年使用天然气![]() 立方米,则需缴纳天然气费为_____元(直接写出结果).
立方米,则需缴纳天然气费为_____元(直接写出结果).
![]()
![]() 年使用天然气
年使用天然气![]() 立方米,则小红家
立方米,则小红家![]() 年需缴纳的天然气费为多少元?
年需缴纳的天然气费为多少元?
![]() 依此方案计算,若王先生家
依此方案计算,若王先生家![]() 年实际缴纳天然气费
年实际缴纳天然气费![]() 元,求该户
元,求该户![]() 年使用天然气多少立方米?
年使用天然气多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
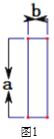
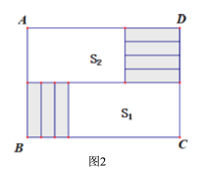
【题目】将7张相同的长方形纸片(如图1)按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分恰好可以分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,S1-S2=______.
(2)当AD=30时,用含a,b的式子表示S1-S2.
(3)若AB长度不变,AD变长,将这7张小长方形纸片按照同样的方式放在新的长方形ABCD内,而且S1-S2的值总保持不变,则a,b满足的关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遵义市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:
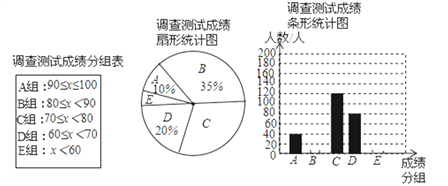
(1)参加调查测试的学生为多少人?
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在哪组内?
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
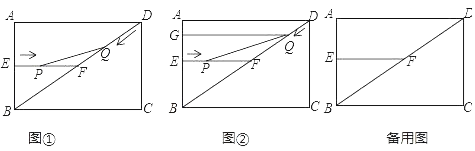
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com