
【题目】将7张相同的长方形纸片(如图1)按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分恰好可以分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,S1-S2=______.
(2)当AD=30时,用含a,b的式子表示S1-S2.
(3)若AB长度不变,AD变长,将这7张小长方形纸片按照同样的方式放在新的长方形ABCD内,而且S1-S2的值总保持不变,则a,b满足的关系是______.
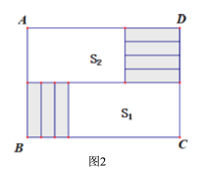
【答案】(1)48;(2)30a-120b+ab;(3)a=4b.
【解析】
(1)观察图形,分别求出S1和S2的面积,再求差即可;
(2)用含a、b的代数式分别表示S1和S2的面积,再求差即可;
(3)设AD=m, 用含a、b、m的代数式分别表示S1和S2的面积差,再去括号合并同类项,根据题意S1-S2的值总保持不变,即可解答.
(1)解:当a=9,b=2,AD=30时,S1=a(30-3b)=9×(30-3×2)=216
S2=4b(30-a)=4×2×(30-9)=168
S1-S2=216-168=48
(2)解:S1-S2
=a(30-3b)-4b(30-a)
=30a-120b+ab
(3)解:设AD=m,
S1-S2
=(am-3ab)-(4bm-4ab)
=am-4bm+ab
若S1-S2的值总保持不变,则S1-S2的值与m的取值无关,所以有am-4bm=0
则a=4b.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
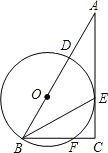
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
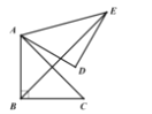
【题目】如图,在Rt△ABC中,∠ABC=90,AB=BC=![]() ,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,求BE的长为( )
,将△ABC绕点A逆时针旋转60,得到△ADE,连接BE,求BE的长为( )
A. 2+![]() B. 2
B. 2![]() C. 2+2
C. 2+2![]() D. 2
D. 2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,已知△ABC,
(1)△ABC与△A1B1C1关于原点O对称,写出△A1B1C1各顶点的坐标,画出△A1B1C1;
(2)以O为旋转中心将△ABC顺时针旋转90°得△A2B2C2,画出△A2B2C2并写出△A2B2C2各顶点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
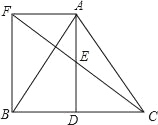
【题目】如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
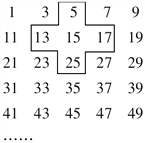
【题目】将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
(1)十字框中的五个数的和与中间数15有什么关系?
(2)设中间数为![]() ,求出十字框中五个数之和;
,求出十字框中五个数之和;
(3)十字框中五个数之和能等于2 015吗?若能,请写出这五个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
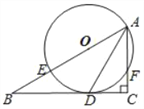
【题目】已知△ABC中∠ACB=90°,E在AB上,以AE为直径的⊙O与BC相切于D,与AC相交于F,连接AD.
(1)求证:AD平分∠BAC;
(2)连接OC,如果∠B=30°,CF=1,求OC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com