
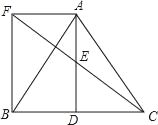
【题目】如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.
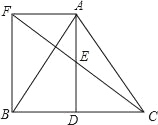
【答案】(1)证明见解析;(2)若AB=AC,则四边形AFBD是矩形.理由见解析.
【解析】分析:(1)因为AF∥BC,E为AD的中点,即可根据AAS证明△AEF≌△DEC,故有BD=DC;
(2)由(1)知,AF=DC且AF∥DC,可得四边形AFDC是平行四边形,又因为AD=CF,故可根据对角线相等的平行四边形是矩形进行判定.
详解:(1)证明:∵AF∥BC,
∴∠AFE=∠DCE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△DEC中,
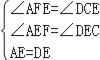 ,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴CD=BD,
∴D是BC的中点;
(2)解:若AB=AC,则四边形AFBD是矩形.理由如下:
∵△AEF≌△DEC,
∴AF=CD,
∵AF=BD,
∴CD=BD;
∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
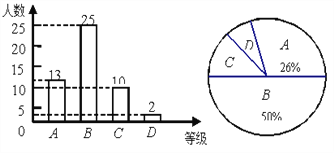
【题目】某一中学以1班学生的地理测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制成两幅统计图,结合图中信息解答下列问题:
(1)D级学生的人数占全班人数的百分比为________;
(2)扇形统计图中C级所在扇形圆心角度数为__________;
(3)若该校共有1500人,则估计该校地理成绩得A级的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有200名学生,为了向市团委推荐本年级一名学生参加团代会,按如下程序进行了民主投票,推荐的程序如下:首先由全年级学生对六名候选人进行投票,每名学生只能给一名候选人投票,选出票数多的前三名;然后再对这三名候选人(记为甲、乙、丙)进行笔试和面试.两个程序的结果统计如下:

测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 92 | 90 | 95 |
面试 | 85 | 95 | 80 |
请你根据以上信息解答下列问题:
(1)请分别计算甲、乙、丙的得票数;
(2)若规定每名候选人得一票记1分,将投票、笔试、面试三项得分按照2:5:3的比例计入每名候选人的总成绩,成绩最高的将被推荐,请通过计算说明甲、乙、丙哪名学生将被推荐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市近期公布的居民用天然气阶梯价格听证会方案如下:
第一档天然气用量 | 第二档天然气用量 | 第三档天然气用量 |
年用天然气量 | 年用天然气量超出 | 年用天然气量 |
例:若某户![]() 年使用天气然
年使用天气然![]() 立方米,按该方案计算,则需缴纳天然气费为:
立方米,按该方案计算,则需缴纳天然气费为:![]() ×
×![]() +
+![]() ×(
×(![]() -
-![]() )=
)=![]() (元);依此方案请回答:
(元);依此方案请回答:
![]() 若小明家
若小明家![]() 年使用天然气
年使用天然气![]() 立方米,则需缴纳天然气费为_____元(直接写出结果).
立方米,则需缴纳天然气费为_____元(直接写出结果).
![]()
![]() 年使用天然气
年使用天然气![]() 立方米,则小红家
立方米,则小红家![]() 年需缴纳的天然气费为多少元?
年需缴纳的天然气费为多少元?
![]() 依此方案计算,若王先生家
依此方案计算,若王先生家![]() 年实际缴纳天然气费
年实际缴纳天然气费![]() 元,求该户
元,求该户![]() 年使用天然气多少立方米?
年使用天然气多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
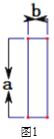
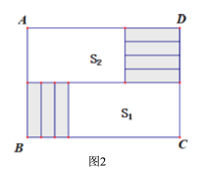
【题目】将7张相同的长方形纸片(如图1)按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分恰好可以分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.
(1)当a=9,b=2,AD=30时,S1-S2=______.
(2)当AD=30时,用含a,b的式子表示S1-S2.
(3)若AB长度不变,AD变长,将这7张小长方形纸片按照同样的方式放在新的长方形ABCD内,而且S1-S2的值总保持不变,则a,b满足的关系是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了顺利通过“国家文明城市”验收,市政府拟对部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完成工程,又能使工程费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】遵义市某中学为了搞好“创建全国文明城市”的宣传活动,对本校部分学生(随机抽查)进行了一次相关知识了解程度的调查测试(成绩分为A、B、C、D、E五个组,x表示测试成绩).通过对测试成绩的分析,得到如图所示的两幅不完整的统计图.请你根据图中提供的信息解答以下问题:
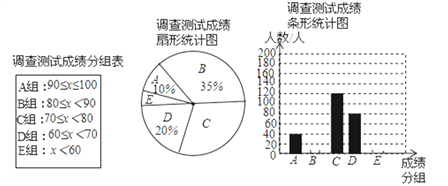
(1)参加调查测试的学生为多少人?
(2)将条形统计图补充完整;
(3)本次调查测试成绩中的中位数落在哪组内?
(4)若测试成绩在80分以上(含80分)为优秀,该中学共有学生2600人,请你根据样本数据估计全校学生测试成绩为优秀的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家今年3月份两次同时购进了甲、乙两种不同单价的糖果,第一次购买甲种糖果的数量比乙种糖果的数量多50%,第二次购买甲种糖果的数量比第一次购买甲种糖果的数量少60%,结果第二次购买糖果的总数量虽然比第一次购买糖果的总数量多20%,但第二次购买甲乙糖果的总费用却比第一次购买甲乙糖果的总费用费少10%.(甲,乙两种糖果的单价不变),则乙种糖果的单价是甲种糖果单价的_____%.
查看答案和解析>>
科目:初中数学 来源: 题型:
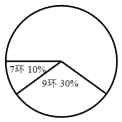
【题目】在全运会射击比赛的选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
命中环数 | 10 | 9 | 8 | 7 |
命中次数 | 3 | 2 |
(1)根据统计表(图)中提供的信息,补全统计表及扇形统计图;
(2)已知乙运动员10次射击的平均成绩为9环,方差为1.2,如果只能选一人参加比赛,你认为应该派谁去?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com