练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

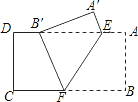
    【题目】如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B'处，点A落在点A'处．

    （1）求证：B'E＝BF；

    （2）若AE＝1，B'E＝2，求梯形ABFE的面积．

    【答案】（1）见解析；（2）

    【解析】

    （1）由折叠可得，BF＝，依据，可得B'F＝B'E，进而得到；

    （2）由折叠可得，，，根据勾股定理可得A'B'的长，再根据梯形面积计算公式，即可得到梯形ABFE的面积．

    解：（1）由折叠可得，BF＝B'F，∠BFE＝∠B'FE，

    由AD∥BC，可得∠B'EF＝∠BFE，

    ∴∠B'EF＝∠BFE，

    ∴B'F＝B'E，

    ∴B'E＝BF；

    （2）由折叠可得，，，而B'E＝BF＝2，

    ∴A'B'＝＝＝，

    ∴AB＝，

    ∴梯形ABFE的面积＝＝＝．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形OABC中，点O为原点，点A的坐标为（0，8），点C的坐标为（6，0）．抛物线y＝﹣x2+bx+c经过点A、C，与AB交于点D．

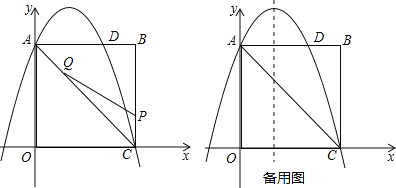
    （1）求抛物线的函数解析式；

    （2）点P为线段BC上一个动点（不与点C重合），点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．

    ①求S关于m的函数表达式；

    ②当S最大时，在抛物线y＝﹣x2+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点F从菱形ABCD的顶点A出发，沿A→D→B以1cm/s的速度匀速运动到点B，图2是点F运动时，△FBC的面积y（cm2）随时间x（s）变化的关系图象，则a的值为（　　）

    A. B. 2 C. D. 2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴相交于、两点，与轴相交于点，且点与点的坐标分别为．，点是抛物线的顶点．点为线段上一个动点，过点作轴于点，若．

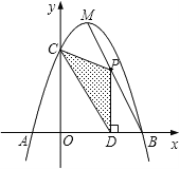
    （1）求二次函数解析式；

    （2）设的面积为，试判断有最大值或最小值？若有，求出其最值，若没有，请说明理由；

    （3）在上是否存在点，使为直角三角形？若存在，请写出点的坐标若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

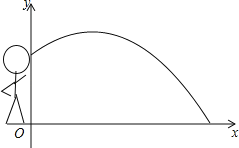
    【题目】如图，一名运动员推铅球，已知铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系始终是y＝ax2+x+（a为常数，a＜0）．

    （1）解释上述函数表达式中“”的实际意义；

    （2）当a＝﹣时，这名运动员能把铅球推出多远？

    （3）若这名运动员某次将铅球推出的距离不小于（2）中的距离，写出此时a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

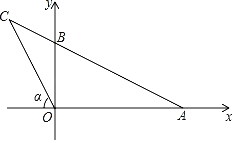
    【题目】如图，在平面直角坐标系中，AB=3，连结AB并延长至C，连结OC，若满足OC2=BCAC，tanα=2，则点C的坐标为(　　)

    A.(﹣2，4)B.(﹣3，6)C.(﹣，)D.(﹣，)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

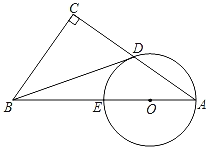
    【题目】如图，在Rt△ABC中，∠C=90°，O在AB上，以O为圆心，以OA长为半径的圆分别与AC，AB交于点D，E，直线BD与⊙O相切于点 D．

    (1)求证：∠CBD=∠A；

    (2)若AC=6，AD：BC=1:．

    ①求线段BD的长；

    ②求⊙O的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中（如图），已知经过点A（﹣3，0）的抛物线y＝ax2+2ax﹣3与y轴交于点C，点B与点A关于该抛物线的对称轴对称，D为该抛物线的顶点．

    （1）直接写出该抛物线的对称轴以及点B的坐标、点C的坐标、点D的坐标；

    （2）联结AD、DC、CB，求四边形ABCD的面积；

    （3）联结AC．如果点E在该抛物线上，过点E作x轴的垂线，垂足为H，线段EH交线段AC于点F．当EF＝2FH时，求点E的坐标．

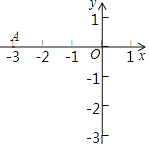
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据交管部门统计，高速公路超速行驶是引发交通事故的主要原因．我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速，渝黔高速公路某路段的限速是：每小时80千米（即最高时速不超过80千米），如图，他们将观测点设在到公路l的距离为0.1千米的P处．这时，一辆轿车由綦江向重庆匀速直线驶来，测得此车从A处行驶到B处所用的时间为3秒（注：3秒＝小时），并测得∠APO＝59°，∠BPO＝45°．试计算AB并判断此车是否超速？（精确到0.001）．（参考数据：sin59°≈0.8572，cos59°≈0.5150，tan59°≈1.6643）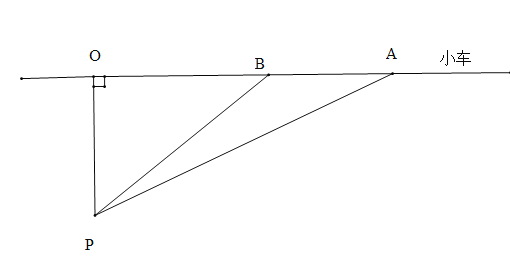

    查看答案和解析>>

    同步练习册答案