练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，矩形纸片ABCD，AB=2，点E在BC上，且AE=EC，若将纸片沿AE折叠，使点B落在AC上，求AE的长．

    分析 根据等腰三角形的性质得到∠EAC=∠ECA，由翻转变换的性质得到∠BAE=∠EAC，根据三角形内角和定理求出∠BAE=30°，根据余弦的概念计算即可．

    解答 解：∵AE=EC，
    ∴∠EAC=∠ECA，
    由翻转变换的性质可知，∠BAE=∠EAC，
    ∴∠EAC=∠ECA=∠BAE，又∠B=90°，
    ∴∠BAE=30°，
    ∴AE=AB÷cos∠BAE=$\frac{4}{3}\sqrt{3}$．

    点评 本题考查的是翻转变换的性质和锐角三角函数的概念，翻转变换是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．下列命题中，正确的是（　　）
    A．菱形的对角线相等
    B．平行四边形既是轴对称图形，又是中心对称图形
    C．正方形的对角线相等且互相垂直
    D．矩形的对角线不能相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．要使$\frac{（m-2）x}{（2-m）（1-x）}$=$\frac{x}{x-1}$恒成立，则（　　）
    A．m=2B．m＞2C．m＜2D．m≠2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．计算下列各式，并探求规律：
    （x-1）（x+1）=x2-1；
    （x-1）（x2+x+1）=x3-1；
    （x-1）（x3+x2+x+1）=x4-1；
    …
    根据你前面计算各式的结果所发现的规律，猜想：
    （x-1）（xn-1+xn-2+…+x2+x+1）=xn-1．（其中n为正整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）4ab3•$\frac{-3a}{{2b}^{3}}$；
    （2）$\frac{8}{{x}^{3}}$÷$\frac{36}{{x}^{2}}$；
    （3）$\frac{a^2-4b^2}{4ab^2}$．$\frac{ab}{a+2b}$；
    （4）$\frac{a^2-b^2}{2ab}$÷（a+b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

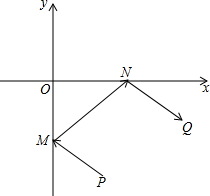    17．牧马人某天要从马厩牵出马，先到草地边的某一处牧马，再到河边饮水，然后回到帐篷，为了便于研究，以河边为x轴、草地边为y轴建立平面直角坐标系，如图所示，马厩P的坐标为（2，-4），帐篷Q的坐标为（6，-2），请你帮他确定这一天的最短路线．
    （1）请你作出最短路线并简要说明作法；
    （2）求最短路线中草地边的牧马点M和河边饮水点N的坐标；
    （3）求这个最短路线的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，在△ABC中，∠ACB=90°，点O是三角形内的一点，且S△OAB=S△OBC=S△OAC，那么$\frac{O{A}^{2}+O{B}^{2}}{O{C}^{2}}$值为5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，DC是以AB为直径的半圆上的弦，DM⊥CD交AB于点M，CN⊥CD交AB于点N．AB=10，CD=6．则四边形DMNC的面积（　　）
    A．等于24B．最小为24C．等于48D．最大为48

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

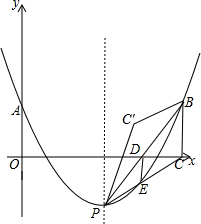    20．如图，抛物线y=a（x-$\sqrt{2}$m）2-m（其中m＞1）与其对称轴l相交于点P，与y轴相交于点A（0，m）．点A关于直线l的对称点为B，作BC⊥x轴于点C，连接PC、PB，与抛物线、x轴分别相交于点D、E，连接DE．将△PBC沿直线PB翻折，得到△PBC′．
    （1）该抛物线的解析式为y=$\frac{1}{m}（x-\sqrt{2}m）^{2}-m$；（用含m的式子表示）；
    （2）探究线段DE、BC的关系，并证明你的结论；
    （3）直接写出C′点的坐标（用含m的式子表示）．

    查看答案和解析>>

    同步练习册答案