
【题目】如图,观察每个正多边形中![]() 的变化情况,解答下列问题:
的变化情况,解答下列问题:
 ……
……
(1)将下面的表格补充完整:
正多边形的边数 | 3 | 4 | 5 | 6 | …… |
|
| _________ | _________ | _________ | _________ | …… | _________ |
(2)根据规律,是否存在一个正![]() 边形,使其中的
边形,使其中的![]() ?若存在,写出
?若存在,写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)根据规律,是否存在一个正![]() 边形,使其中的
边形,使其中的![]() ?若存在,写出
?若存在,写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)60°,45°,36°,30°,![]() ;(2)当多边形是正九边形,能使其中的
;(2)当多边形是正九边形,能使其中的![]() ;(3)不存在,理由见解析.
;(3)不存在,理由见解析.
【解析】
(1)首先根据多边形的内角公式:(n-2)×180°,将n=3、4、5、6、8、12代入公式分别计算出各多边形的内角和;然后再根据多边形的外角和为360°,即可得到各多边形的内角和,进而完成表格.(2)依据题意得∠α=20°=![]() ,即可求出n的值。(3)依据题意∠α=21°=
,即可求出n的值。(3)依据题意∠α=21°=![]() ,求出n的值是否为正整数即可.
,求出n的值是否为正整数即可.
解:(1)填表如下:
正多边形的边数 | 3 | 4 | 5 | 6 | …… | n |
|
|
|
|
| …… |
|
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(可以观察归纳出来,也可以计算出来).
;(可以观察归纳出来,也可以计算出来).
(2)存在一个正![]() 边形,使其中的
边形,使其中的![]()
理由是:根据题意得:![]() ,
,
解得:![]() ,
,
即当多边形是正九边形,能使其中的![]() ;
;
(3)不存在,理由如下:
假设存在正![]() 边形使得
边形使得![]() ,得
,得![]() ,
,
解得:![]() ,与
,与![]() 是正整数矛盾,
是正整数矛盾,
所以不存在正![]() 边形使得
边形使得![]() .
.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.

(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
【答案】(1)5+3![]() ;(2)3.
;(2)3.
【解析】试题分析:(1)构造直角三角形,AB=![]() 且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
(2)先构造一个45°角,再利用面积是3,可画出图象.
试题解析:
(1)解:如图1所示:△ABC即为所求,
△ABC的周长为: ![]() +2
+2![]() +5=5+3
+5=5+3![]() ;
;

(2)解:如图2所示:△ABD中,∠ADB=45°,且面积为3.

【题型】解答题
【结束】
23
【题目】为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:

(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
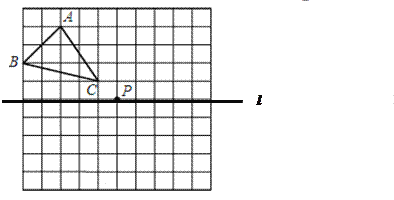
【题目】如图,一个10×10网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线l的对称的△A1B1C1.
(2)画出△ABC关于点P的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形_______________(是或否)轴对称图形,如果是轴对称图形,请画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个数的平方等于![]() ,记为
,记为![]() ,这个数
,这个数![]() 叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为
叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为![]() (
(![]() 为实数),
为实数),![]() 叫这个复数的实部,
叫这个复数的实部, ![]() 叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算: ![]()
(1)填空: ![]() =_________,
=_________, ![]() =____________.
=____________.
(2)填空:①![]() _________; ②
_________; ②![]() _________ .
_________ .
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下列问题:已知, ![]() ,(
,( ![]() 为实数),求
为实数),求![]() 的值.
的值.
(4)试一试:请利用以前学习的有关知识将![]() 化简成
化简成![]() 的形式.
的形式.
(5)解方程:x2 - 2x +4 = 0
查看答案和解析>>
科目:初中数学 来源: 题型:
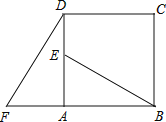
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F,AB=6cm,AD=8cm.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连结FG交BD于点O.判断四边形FBGD的形状,并说明理由.
(3)在(2)的条件下,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点B与点D重合,折痕为EF.
(1)求证:BE=BF;
(2)求△ABE的面积;
(3)求折痕EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
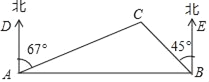
【题目】一艘救生船在码头A接到小岛C处一艘渔船的求救信号,立即出发,沿北偏东67°方向航行10海里到达小岛C处,将人员撤离到码头A张东方向的码头B,测得小岛C位于码头B西北方向,求码头B与小岛C的距离(结果精确到0.1海里).【参考数据:sin23°=0.39,cos23°=0.92,tan23°=0.42, ![]() =1.41】
=1.41】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com