
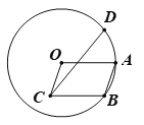
【题目】如图,点A、B在半径为3的⊙O上,以OA、AB为邻边作平行四边形OCBA,作点B关于OA的对称点D,连接CD,则CD的最大值为________.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为了了解某校新初三暑期阅读课外书的情况,某研究小组随机采访该校新九年级的20位同学,得到这20位同学暑期读课外书册数的统计如下:
册数 | 0 | 2 | 3 | 5 | 6 | 8 | 10 |
人数 | 1 | 2 | 4 | 8 | 2 | 2 | 1 |
(1)这20位同学暑期看课外书册数的中位数是 册,众数是 册,平均数是 册。
(2)若小明同学把册数中的数据“8”看成了“7”,那么中位数,众数,平均数中不受影响的是。
(3)若该校有600名新初三学生,试估计该校新初三学生暑期阅读课外书的总册数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接着汉口集家咀的江汉三桥(晴川桥),是一座下承式钢管混凝土系杆拱桥.它犹如一道美丽的彩虹跨越汉江,是江城武汉的一道靓丽景观.桥的拱肋ACB视为抛物线的一部分,桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,相邻系杆之间的间距均为5米(不考虑系杆的粗细),拱肋的跨度AB为280米,距离拱肋的右端70米处的系杆EF的长度为42米.以AB所在直线为x轴,抛物线的对称轴为y轴建立如图②所示的平面直角坐标系.
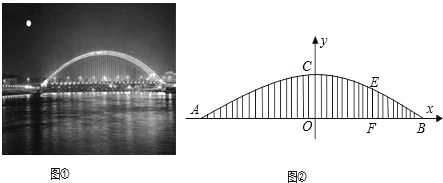
(1)求抛物线的解析式;
(2)正中间系杆OC的长度是多少米?是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
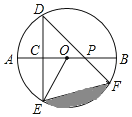
【题目】如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EF、EO,若DE=2,∠DPA=45°.
(1)求⊙O的半径;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,OC∥AD,AD交BC的延长线于D,AB交OC于E.

(1)求证:AD是⊙O的切线;
(2)若⊙O的直径为6,线段BC=2,求∠BAC的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.设运动时间为t秒.
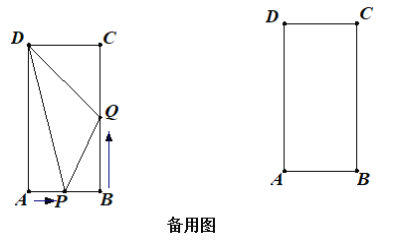
(1)当t=2时,△DPQ的面积为 cm2;
(2)在运动过程中△DPQ的面积能否为26cm2?如果能,求出t的值,若不能,请说明理由;
(3)运动过程中,当 A、P、Q、D四点恰好在同一个圆上时,求t的值;
(4)运动过程中,当以Q为圆心,QP为半径的圆,与矩形ABCD的边共有4个交点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展了“手机伴我健康行”主题活动。他们随即抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人。
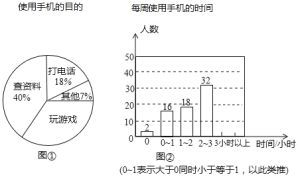
请你根据以上信息解答下列问题:
(1) 在扇形统计图中,“玩游戏”对应的百分比为___,圆心角度数是___度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2小时以上(不含2小时)的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com