
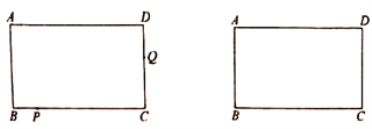
【题目】已知:如图,在长方形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 方向向点
方向向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿
的速度沿![]() 向点
向点![]() 运动,
运动,![]() 同时出发,当点
同时出发,当点![]() 停止运动时,点
停止运动时,点![]() 也随之停止,设点
也随之停止,设点![]() 运动的时间为
运动的时间为![]() 秒.请回答下列问题:
秒.请回答下列问题:
(1)请用含![]() 的式子表达
的式子表达![]() 的面积
的面积![]() ,并直接写出
,并直接写出![]() 的取值范围.
的取值范围.
(2)是否存在某个![]() 值,使得
值,使得![]() 和
和![]() 全等?若存在,请求出所有满足条件的
全等?若存在,请求出所有满足条件的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.
【答案】(1)![]() (0<t≤1.5),
(0<t≤1.5),![]() (1.5<t≤4),
(1.5<t≤4),![]() (4<t<5);(2)当t=3时,△ABP和△CDQ全等.
(4<t<5);(2)当t=3时,△ABP和△CDQ全等.
【解析】
(1)分别讨论①当Q在CD上时,②当Q在DA上时, ③当Q在AB上时,表示出CQ,BP求出面积即可;
(2)分别讨论①当Q在CD上时,②当Q在AD上时,③当Q在AB上时,求出△ABP和△CDQ全等时的t值.
解:(1)①当Q在CD上时,
如图,由题意得CQ=2t,BP=t
∴CP=5t(0<t≤1.5)![]()
②当Q在DA上时,(1.5<t≤4)
![]()
![]()
![]()
③当Q在AB上时,由题意得BQ=112t(4<t<5)
![]()
![]()
![]()
(2)①当Q在CD上时,不存在t使△ABP和△CDQ全等
②当Q在AD上时,
如图,由题意得DQ=2t3
要使△ABP≌△CDQ,则需BP=DQ
∵DQ=2t3,BP=t
∴t=2t3,t=3
即当t=3时,△ABP≌△CDQ.
③当Q在AB上时,不存在t使△ABP和△CDQ全等
综上所述,当t=3时,△ABP和△CDQ全等.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 过点
过点![]() 且与
且与![]() 轴交于点
轴交于点![]() ,点
,点![]() 关于
关于![]() 轴的对称点为点
轴的对称点为点![]() .过点
.过点![]() 且与直线
且与直线![]() 平行的直线交
平行的直线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
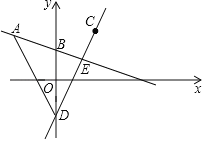
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是 ( )
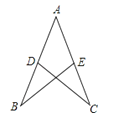
A. AB=AC B. ∠ADC=∠AEB C. ∠B=∠C D. BE=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
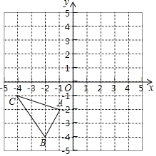
【题目】如图,在平面直角坐标系中,![]() 的三个顶点分别为
的三个顶点分别为![]() ,
,![]() ,
,![]() .
.
![]() 把
把![]() 向上平移
向上平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
![]() 已知点
已知点![]() 与点
与点![]() 关于直线
关于直线![]() 成轴对称,请画出直线
成轴对称,请画出直线![]() 及
及![]() 关于直线
关于直线![]() 对称的
对称的![]() .
.
![]() 在
在![]() 轴上存在一点
轴上存在一点![]() ,满足点
,满足点![]() 到点
到点![]() 与点
与点![]() 距离之和最小,请直接写出
距离之和最小,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
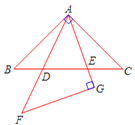
【题目】如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,AF、AG与边BC的交点分别为D、E (点D不与点B重合,点E不与点C重合).
(1)图中共有 对相似而不全等的三角形.
(2)选取其中一对进行证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解初中学生每天在校体育活动的时间(单位:h),随机调査了该校的部分初中学生.根据调查结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
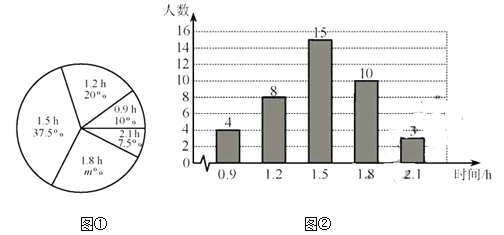
(Ⅰ)本次接受调查的初中学生人数为___________,图①中m的值为_____________;
(Ⅱ)求统计的这组每天在校体育活动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每天在校体育活动时间的样本数据,若该校共有800名初中学生,估计该校每天在校体育活动时间大于1h的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
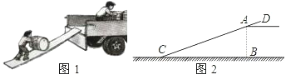
【题目】如图1是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图2中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,请求出木板CD的长度?
(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
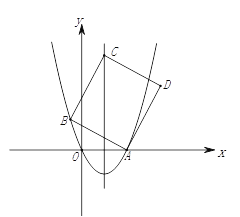
【题目】如图,抛物线![]() 交x轴的正半轴于点A,点B(
交x轴的正半轴于点A,点B(![]() ,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
,a)在抛物线上,点C是抛物线对称轴上的一点,连接AB、BC,以AB、BC为邻边作□ABCD,记点C纵坐标为n,
(1)求a的值及点A的坐标;
(2)当点D恰好落在抛物线上时,求n的值;
(3)记CD与抛物线的交点为E,连接AE,BE,当△AEB的面积为7时,n=___________.(直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com