如图1，在平面直角坐标系xOy中，直线l：
与x轴、y轴分别交于点A和点B（0，﹣1），抛物线
经过点B，且与直线l的另一个交点为C（4，n）．
（1）求n的值和抛物线的解析式；
（2）点D在抛物线上，且点D的横坐标为t（0＜t＜4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值；
（3）M是平面内一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．
科目：初中数学 来源：山东省临沭县2018-2019学年七年级上学期期中考试数学试卷 题型：解答题
对于有理数a、b，定义一种新运算“⊙”，规定：a⊙b＝|a+b|+|a﹣b|．
(1)计算2⊙（-4）的值；
(2)若a，b在数轴上的位置如图所示，化简a⊙b．
查看答案和解析>>
科目：初中数学 来源：山东省枣庄市2018届中考数学模拟试卷（5月份） 题型：单选题
在平面直角坐标系xOy中，将点N（–1，–2）绕点O旋转180°，得到的对应点的坐标是
A. （1，2） B. （–1，2）
C. （–1，–2） D. （1，–2）
查看答案和解析>>
科目：初中数学 来源：人教版九年级数学上册 第２2章《二次函数》经典题型单元测试卷 题型：单选题
如图，在平面直角坐标系中，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0）、B（3，0），与y轴交于点C，顶点为D，对称轴为直线x=1，有下列四个判断：
①关于x的一元二次方程ax2+bx+c=0的两个根分别是x1=﹣1，x2=3；
②a﹣b+c=0；
③若抛物线上有三个点分别为（﹣2，y1）、（1，y2）、（2，y3），则y1＜y2＜y3；
④当OC=3时，点P为抛物线对称轴上的一个动点，则△PCA的周长的最小值是
，
上述四个判断中正确的 有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源：人教版九年级数学上册 第２2章《二次函数》经典题型单元测试卷 题型：单选题
已知二次函数y=x2﹣bx+2（﹣2≤b≤2），当b从﹣2逐渐增加到2的过程中，它所对应的抛物线的位置也随之变动，下列关于抛物线的移动方向的描述中，正确的是（ ）
A. 先往左上方移动，再往左下方移动
B. 先往左下方移动，再往左上方移动
C. 先往右上方移动，再往右下方移动
D. 先往右下方移动，再往右上方移动
查看答案和解析>>
科目：初中数学 来源：北师大版2018-2019年九年级数学下册 第２章《二次函数》经典题型单元测试卷 题型：解答题
已知二次函数y=x2﹣2x﹣1．
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
（1）请在表内的空格中填入适当的数；
（2）根据列表，请在所给的平面直角坐标系中画出y=x2﹣2x﹣1的图象；
（3）当x在什么范围内时，y随x增大而减小；
查看答案和解析>>
科目：初中数学 来源：北师大版2018-2019年九年级数学下册 第２章《二次函数》经典题型单元测试卷 题型：单选题
二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：①4a+b=0②9a+c＞3b；③8a+7b+2c＞0④若点A（﹣3，y1），点B（﹣2，y2），点C（8，y3）在该函数图象上，则y1＜y3＜y2⑤若方程a（x﹣1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣l＜5＜x2，其中正确的结论有（ ）
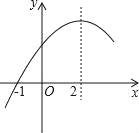
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源：2019届九年级苏科版数学下册 第5章《二次函数》经典题型单元测试卷 题型：解答题
已知函数y=
x2，y=（x+2）2+2和y=（x+2）2﹣3．
（1）在同一个平面直角坐标系中画出这三个函数的图象；
（2）当图中二次函数的函数值y随x的增大而同时增大时，求x的取值范围；当函数值y随x的增大面同时减小时，求x的取值范围．（直接写答案）
查看答案和解析>>
科目：初中数学 来源：华东师大版2019届九年级数学下册 第 2 6 章《二次函数》经典题型单元测试卷 题型：单选题
抛物线y=（m+1）x2﹣2x+m2﹣1经过原点，则m的值为（ ）
A. 0 B. 1 C. ﹣1 D. ±1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
