
【题目】反比例函数![]() 与一次函数y=k(x+1)(其中x为自变量,k为常数)在同一坐标系中的图象可能是( )
与一次函数y=k(x+1)(其中x为自变量,k为常数)在同一坐标系中的图象可能是( )
A.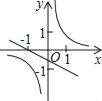 B.
B.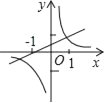 C.
C.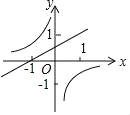 D.
D.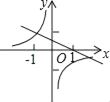
【答案】C
【解析】
分别根据反比例函数与一次函数的性质对各选项进行逐一分析即可.
解:一次函数![]() 可化为
可化为![]() ,即一次函数在y轴上的截距为k,
,即一次函数在y轴上的截距为k,
A、由反比例函数的图象可知,k>0,由一次函数的图象可知k<0,由一次函数在y轴上的截距可知k<0,两结论矛盾,故本选项错误;
B、由反比例函数的图象可知,k-1>0,即k>1,由一次函数的图象可知0<k<1,两结论矛盾,故本选项错误;
C、由反比例函数的图象可知k-1<0,即k<1,由一次函数的图象可知k>0,当x=-1时,y=0,故0<k<1,两结论一致,故本选项正确确;
D、由反比例函数的图象可知,k<0,由一次函数的图象可知k<0,由一次函数在y轴上的截距可知k>0,两结论矛盾,故本选项错误.
故选:C.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
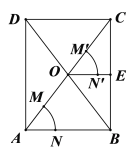
【题目】如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).

A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 内接于
内接于![]() ,
,![]() 是直径,点
是直径,点![]() 在
在![]() 上,
上,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 交
交![]() 边于点
边于点![]() .
.
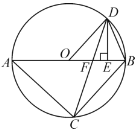
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() ,求四边形
,求四边形![]() 的面积(用含有
的面积(用含有![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列要求,解答相关问题:
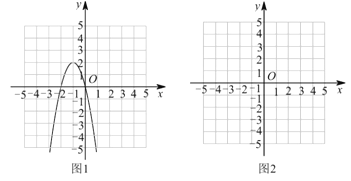
(1)请补全以下求不等式![]() 的解集的过程:
的解集的过程:
①构造函数,画出图象:根据不等式特征构造二次函数![]() ;抛物线的对称轴为_________,开口向下,顶点坐标为__________,与
;抛物线的对称轴为_________,开口向下,顶点坐标为__________,与![]() 轴的交点是_________,用三点法画出二次函数
轴的交点是_________,用三点法画出二次函数![]() 的图象如图1所示;
的图象如图1所示;
②数形结合,求得界点:当![]() 时,求得方程
时,求得方程![]() 的解为___________;
的解为___________;
③借助图象,写出解集:由图象可得不等式![]() 的解集为_________.
的解集为_________.
(2)利用(1)中求不等式解集的方法步骤,求不等式![]() 的解集.
的解集.
①构造函数,画出![]() 的图象(在图2中画出);
的图象(在图2中画出);
②数形结合,求得界点:当![]() __________时,求得方程
__________时,求得方程![]() 的解为__________;
的解为__________;
③借助图象,写出解集.由图2知,不等式![]() 的解集是__________.
的解集是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BC是⊙O的直径,弦AF交BC于点E,∠CAF=2∠B.
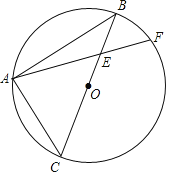
(1)求证:AE=AC;
(2)若⊙O的半径为4,E是OB的中点,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师随机抽查了本学期学生读课外书册数的情况,绘制成条形图(图1)和不完整的扇形图(图2),其中条形图被墨迹遮盖了一部分.
(1)求条形图中被遮盖的数,并写出册数的中位数;
(2)在所抽查的学生中随机选一人谈读书感想,求选中读书超过5册的学生的概率;
(3)随后又补查了另外几人,得知最少的读了6册,将其与之前的数据合并后,发现册数的中位数没改变,则最多补查了 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费,年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档,某户应交天然气费![]() (元)与年用天然气量
(元)与年用天然气量![]() (立方米)的关系如图所示,观察图像并回答问题:
(立方米)的关系如图所示,观察图像并回答问题:
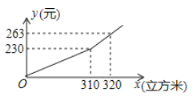
(1)求![]() 与
与![]() 之间的函数解析式并写出自变量
之间的函数解析式并写出自变量![]() 的取值范围;
的取值范围;
(2)嘉琪家2018年天然气费为1029元,求嘉琪家2018年使用天然气量是否超出310立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)
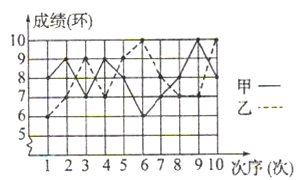
(1)依据折线统计图,得到下面的表格:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中![]() ________,
________,![]() ________;
________;
(2)甲成绩的众数是________环,乙成绩的中位数是________环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com