
【题目】将一个正方形纸片AOBC放置在平面直角坐标系中,点A(0,4),点O(0,0),B(4,0),C(4,4)点.动点E在边AO上,点F在边BC上,沿EF折叠该纸片,使点O的对应点M始终落在边AC上(点M不与A,C重合),点B落在点N处,MN与BC交于点P.
(Ⅰ)如图①,当∠AEM=30°时,求点E的坐标;
(Ⅱ)如图②,当点M落在AC的中点时,求点E的坐标;
(Ⅲ)随着点M在AC边上位置的变化,△MPC的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
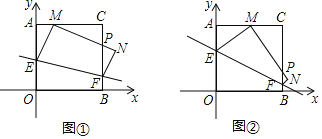
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)△MPC的周长不变,为8,理由见解析
;(Ⅲ)△MPC的周长不变,为8,理由见解析
【解析】
(Ⅰ)由折叠的性质知OE=EM,设OE=x,则EM=OE=x,AE=![]() x,根据等量关系AE+OE=OA列出方程并解答;
x,根据等量关系AE+OE=OA列出方程并解答;
(Ⅱ)由线段中点的定义知AM=![]() AC=2.设OE=m,则EM=OE=m,AE=4﹣m,在Rt△AEM中,由勾股定理列出关于x的方程并解答;
AC=2.设OE=m,则EM=OE=m,AE=4﹣m,在Rt△AEM中,由勾股定理列出关于x的方程并解答;
(Ⅲ)设AM=a,则OE=EM=b,MC=4﹣a,在Rt△AEM中,由勾股定理得出a、b的关系式,可证Rt△AEM∽Rt△CMP,根据相似三角形的周长比等于相似比求△MPC的周长.
解:(Ⅰ)如图①,
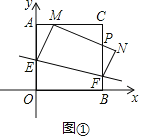
∵四边形ABCD是正方形,
∴∠EAM=90°.
由折叠知OE=EM.
设OE=x,则EM=OE=x,
在Rt△AEM中,cos∠AEM=![]()
∵∠AEM=30°
∴cos30°=![]() =
=![]()
∴AE=![]() x,
x,
∴AE+OE=OA,即![]() x+x=4,
x+x=4,
∴x=16﹣8![]() .
.
∴![]()
(Ⅱ)如图②,
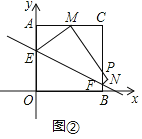
∵点M是边AC的中点,
∴AM=![]() AC=2.
AC=2.
设OE=m,则EM=OE=m,AE=4﹣m,
在Rt△AEM中,EM2=AM2+AE2,
即m 2=22+(4﹣m)2,解得m=![]() .
.
∴![]() ;
;
(Ⅲ)△MPC的周长不变,为8.
理由:设AM=a,OE=EM=b,
∵AC=4
∴MC=4﹣a,
在Rt△AEM中,由勾股定理得AE2+AM2=EM2,
(4﹣b)2+a2=b2,解得16+a2=8b.
∴16﹣a2=8(4﹣b)
∵∠EMP=90°,∠A=∠C,
∴Rt△AEM∽Rt△CMP,
∴![]() ,即
,即![]() ,
,
解得DM+MP+DP=![]() =8.
=8.
∴△CMP的周长为8.


科目:初中数学 来源: 题型:
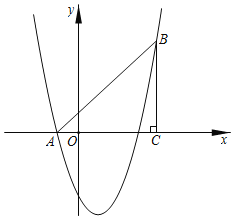
【题目】如图,在平面直角坐标系中,已知A(﹣1,0)、C(4,0),BC⊥x轴于点C,且AC=BC,抛物线y=x2+bx+c经过A、B两点.
(1)求抛物线的表达式;
(2)点E是线段AB上一动点(不与A、B重合),过点E作x轴的垂线,交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形?若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是![]() 米的旗杆
米的旗杆![]() ,从办公楼顶端
,从办公楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是
是![]() ,旗杆底端
,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是
是![]() 米,梯坎坡长
米,梯坎坡长![]() 是
是![]() 米,梯坎坡度
米,梯坎坡度![]() ,求大楼
,求大楼![]() 的高度.(精确到
的高度.(精确到![]() 米,参与数据:
米,参与数据: ![]() ,
, ![]() ,
, ![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() ),以
),以![]() 为旋转中心顺时针旋转矩形
为旋转中心顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() .
.
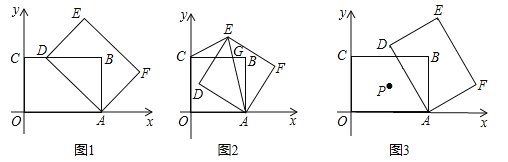
(1)如图1,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的长;
的长;
(2)如图2,当![]() 时,矩形
时,矩形![]() 的对角线
的对角线![]() 交矩形
交矩形![]() 的边
的边![]() 于点
于点![]() ,连结
,连结![]() ,若
,若![]() 是等腰三角形,求直线
是等腰三角形,求直线![]() 的解析式.
的解析式.
(3)如图3,当![]() 时,矩形
时,矩形![]() 的对称中心为点
的对称中心为点![]() .
.![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
查看答案和解析>>
科目:初中数学 来源: 题型:
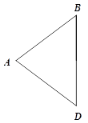
【题目】如图,在△ABD中,∠ABD = ∠ADB,分别以点B,D为圆心,AB长为半径在BD的右侧作弧,两弧交于点C,连接BC,DC和AC,AC与BD交于点O.
(1)用尺规补全图形,并证明四边形ABCD为菱形;
(2)如果AB = 5,![]() ,求BD的长.
,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近一周,各个学校均在紧张有序地进行中考模拟考试,学生们通过模拟考试来调整自己的状态并了解自己的学业水平.某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数,在全年级随机抽取了男.女各40名学生的成绩(满分为80分,女生成绩中最低分为45分),并将数据进行整理分析,给出了下面部分信息:
①男生成绩扇形统计图和女生成绩频数分布直方图如下:(数据分组为A组:x<50;B组:50≤x<60;C组:60≤x<70;D组:70≤x≤80)

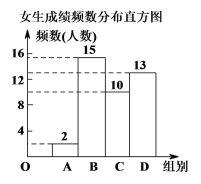
②男生C组中全部15名学生的成绩为:
63,69,64,62,68,69,65,69,65,66,67,61,67,66,69.
③两组数据的平均数.中位数.众数.满分率.极差(单位:分)如下表所示:
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形统计图A组学生中所对应的圆心角α的度数为 ,中位数b= ,众数c= ,极差d= .
(2)通过以上的数据分析,你认为 (填“男生”或“女生”)的物理成绩更好,并说明理由:
① ;② .
(3)若成绩在70分(包含70分)以上为优秀,请你估计该校1200名学生中此次考试中优秀的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com