练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，某办公大楼正前方有一根高度是米的旗杆，从办公楼顶端测得旗杆顶端的俯角是，旗杆底端到大楼前梯坎底边的距离是米，梯坎坡长是米，梯坎坡度，求大楼的高度．（精确到米，参与数据： ， ， ）

    【答案】米

    【解析】延长AB交DC于H，作EG⊥AB于G，则GH=DE=15米，EG=DH，设BH=x米，则CH=x米，在Rt△BCH中，BC=12米，由勾股定理得出方程，解方程求出BH=6米，CH=6米，得出BG、EG的长度，证明△AEG是等腰直角三角形，得出AG=EG=6+20（米），即可得出大楼AB的高度．

    解：在中， ，已知梯坎的坡度．（坡度）∴，由三角函数得，

    ∴．

    由题意可知，四边形为矩形．

    ∴， ．

    ∴．

    在等腰中， ．

    ∴（米）．

    ∴大楼的高度为米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

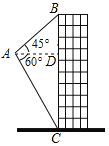
    【题目】如图，航拍无人机从A处测得一幢建筑物顶部B的仰角为45°，测得底部C的俯角为60°，此时航拍无人机与该建筑物的水平距离AD为110m，那么该建筑物的高度BC约为_____m（结果保留整数，≈1.73）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（6分）在一个不透明的口袋装有三个完全相同的小球，分别标号为1、2、3．求下列事件的概率：

    （1）从中任取一球，小球上的数字为偶数；

    （2）从中任取一球，记下数字作为点A的横坐标x，把小球放回袋中，再从中任取一球记下数字作为点A的纵坐标y，点A（x，y）在函数的图象上．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知y关于x的函数表达式是，下列结论不正确的是（ ）

    A.若，函数的最大值是5

    B.若，当时，y随x的增大而增大

    C.无论a为何值时，函数图象一定经过点

    D.无论a为何值时，函数图象与x轴都有两个交点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

    （1）求证：△AEF≌△DEB；

    （2）若∠BAC=90°，求证：四边形ADCF是菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校大课间活动，采用了三种活动形式：足球，排球，篮球，学生选择一种形式参与活动．

    （1）小王对同学们选用的活动形式进行了随机抽样调查，根据调查统计结果，列出了两幅不完整的统计图，利用图中所提供的信息解决以下问题：①小王共调查统计了　　　　人；②请将下图补充完整．

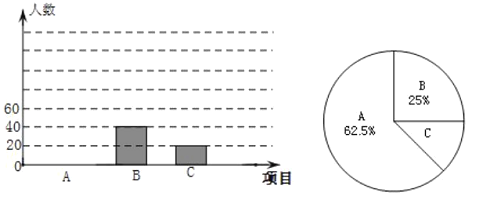
    （2）假设被调查的甲、乙两名同学对这三项活动的选择是等可能的，请你用列表法或画树状图的方法求两人中至少有一个选择的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一个正方形纸片AOBC放置在平面直角坐标系中，点A（0，4），点O（0，0），B（4，0），C（4，4）点．动点E在边AO上，点F在边BC上，沿EF折叠该纸片，使点O的对应点M始终落在边AC上（点M不与A，C重合），点B落在点N处，MN与BC交于点P．

    （Ⅰ）如图①，当∠AEM＝30°时，求点E的坐标；

    （Ⅱ）如图②，当点M落在AC的中点时，求点E的坐标；

    （Ⅲ）随着点M在AC边上位置的变化，△MPC的周长是否发生变化？如变化，简述理由；如不变，直接写出其值．

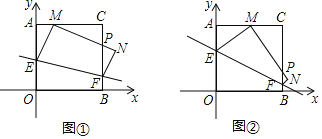
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系xOy中的图形P和直线AB，给出如下定义：M为图形P上任意一点，N为直线AB上任意一点，如果M，N两点间的距离有最小值，那么称这个最小值为图形P和直线AB之间的“确定距离”，记作d（P，直线AB）．

    已知A(2，0)，B(0，2)．

    （1）求d（点O，直线AB）；

    （2）⊙T的圆心为半径为1，若d(⊙T，直线AB)≤1，直接写出t的取值范围；

    （3）记函数的图象为图形Q．若d(Q，直线AB)=1，直接写出k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有甲，乙两种机器人都被用来搬运某体育馆室内装潢材料甲型机器人比乙型机器人每小时少搬运30千克，甲型机器人搬运600千克所用的时间与乙型机器人搬运800千克所用的时间相同，两种机器人每小时分别搬运多少千克？设甲型机器人每小时搬运x千克，根据题意，可列方程为(　　)

    A. ＝B. ＝

    C. ＝D. ＝

    查看答案和解析>>

    同步练习册答案