练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知：如图，平面直角坐标系中，矩形OABC的顶点A(6，0)、B(6，4)，D是BC的中点．动点P从O点出发，以每秒1个单位的速度，沿着OA、AB、BD运动．设P点运动的时间为t秒(0<t<13)．

    (1) 写出△POD的面积S与t之间的函数关系式，并求出△POD的面积等于9时点P的坐标；

    (2) 当点P在OA上运动时，连结CP．问：是否存在某一时刻t，当CP绕点P旋转时，点C能恰好落到AB的中点M处？若存在，请求出t的值并判断此时△CPM的形状；若不存在，请说明理由；

    （3）当点P在AB上运动时，试探索当PO+PD的长最短时的直线PD的表达式。

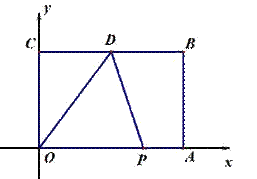                备用图


    分值分配,6+3+2

      

         

      

      （3）  y=-


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，△ABC≌△BAD，A与B，C与D是对应点，若AB=4cm，BD=4.5cm，AD=1.5cm，则BC=__________cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    我市城市居民用电收费方式有以下两种：

    （甲）普通电价：全天0.53元/度；

    （乙）峰谷电价：峰时（早8:00~晚21:00）0.56元/度；

    谷时（晚21:00~早8:00）0.36元/度．

     已知小明家下月计划总用电量为400度，

    （1）若其中峰时电量为100度，则小明家按照哪种方式付电费比较合适？能省多少元？

       （2）峰时电量为多少度时，两种方式所付的电费相等？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


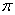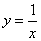    下列函数：①y=－x 2 +2x+1；②y=2r；③；④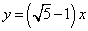；⑤y=－(a+x)(a是常数)；

        ⑥s=6t，其中是一次函数的是______________(填序号)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     如图示，△ABC中点D在边AC上，DB＝BC，E是CD的中点，F是AB的中点.

         求证：EF＝AB.

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若点A（a，b）在反比例函数的图像上，则代数式ab的值为（  ）

    A．0                 B．-2           C． 2              D．-6

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线a∥b，∠1=125°，则∠2的度数为     °．

     


     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


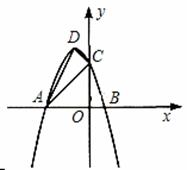
    如图，抛物线y=ax2+bx+c的顶点为D（﹣1，4），与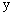轴交于点C（0，3），与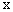轴交于A，B两点（点A在点B的左侧）。

    （1）求抛物线的解析式；

    （2）连接AC，CD，AD，试证明△ACD为直角三角形；

    （3）若点E在抛物线上，EF⊥x轴于点F，以A、E、F为顶点
        的三角形与△ACD相似，直接写出所有满足条件的点E的坐标。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，在△ABC中，AB=AC,AD⊥BC于D，点E、F分别为边AD、CE的中点，且S阴影=4 ㎡，则S△ABC=     　__㎡．

    查看答案和解析>>

    同步练习册答案