
【题目】如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
【答案】
(1)D(-2,3)
(2)![]() 解:设二次函数解析式为:y=ax2+bx+c,
解:设二次函数解析式为:y=ax2+bx+c,
∵A(-3,0),B(1,0),C(0,3),均在函数图像上,
∴ ,
,
∴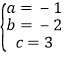 ,
,
∴二次函数的解析式为y=-x2-2x+3.
(3)![]() 解:依题可得:x
解:依题可得:x![]() -2或x
-2或x![]() 1.
1.
【解析】(1)设二次函数解析式为:y=ax2+bx+c,
∵二次函数的图象与x轴交于A(-3,0)、B(1,0)两点,
∴二次函数对称轴x=-![]() =
=![]() =-1,
=-1,
又∵点C、D是二次函数图象上的一对对称点,C(0,3),
设D(x,y),
∴![]() =-1,
=-1,
∴x=-2,y=3,
∴D(-2,3).
(3)由图可得:一次函数值大于二次函数值的x的取值范围为:x![]() -2或x
-2或x![]() 1.
1.
(1)设二次函数解析式为:y=ax2+bx+c,依题可得:二次函数对称轴x=-1,再由点C、D是二次函数图象上的一对对称点得出D点坐标
(2)设二次函数解析式为:y=ax2+bx+c,由题意可得: ,从而求出
,从而求出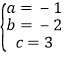 ,从而得出二次函数的解析式.
,从而得出二次函数的解析式.
(3)由图即可得一次函数值大于二次函数值的x的取值范围.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
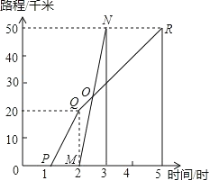
【题目】如图所示 A、B 两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地.如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
(1)甲乙两人中, 先出发,先出发 小时.
(2)甲乙两人中, 先到达B地,先到 小时.
(3)分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
(4)乙出发大约用多长时间就追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=mx2﹣6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥ x轴,交该抛物线于M、N两点,交⊙ P与E、F两点,若EF=2 ![]() ,则MN的长是 .
,则MN的长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一项工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天,需付甲工程队工程款![]() 万元,乙工程队工程款
万元,乙工程队工程款![]() 万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用
万元,工程领导小组根据甲乙两队的投标书测算,可有三种施工方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用![]() 天;③若甲乙两队合作
天;③若甲乙两队合作![]() 天,余下的工程由乙队单独也正好如期完成.
天,余下的工程由乙队单独也正好如期完成.
(1)甲、乙单独完成各需要多少天?
(2)在不耽误工期的情况下,你觉得那一种施工方案最节省工程款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)若正方形ABCD的面积16,CF=3,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查,下面试根据收集的数据绘制的统计图(不完整):
(1)参加抽样调查的学生数是______人,扇形统计图中“大排”部分的圆心角是______°;
(2)把条形统计图补充完整;
(3)若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com