
【题目】如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
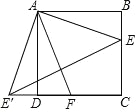
A.△AEE′是等腰直角三角形 B.AF垂直平分EE'
C.△E′EC∽△AFD D.△AE′F是等腰三角形
【答案】D.
【解析】
试题分析:因为将△ABE绕点A顺时针旋转90°,使点E落在点E'处,
∴AE′=AE,∠E′AE=90°,∴△AEE′是等腰直角三角形,故A正确;
∵将△ABE绕点A顺时针旋转90°,使点E落在点E'处,∴∠E′AD=∠BAE,
∵四边形ABCD是正方形,∴∠DAB=90°,∵∠EAF=45°,∴∠BAE+∠DAF=45°,
∴∠E′AD+∠FAD=45°,∴∠E′AF=∠EAF,∵AE′=AE,∴AF垂直平分EE',故B正确;
∵AF⊥E′E,∠ADF=90°,∴∠FE′E+∠AFD=∠AFD+∠DAF,∴∠FE′E=∠DAF,
∴△E′EC∽△AFD,故C正确;∵AD⊥E′F,但∠E′AD不一定等于∠DAE′,
∴△AE′F不一定是等腰三角形,故D错误;
故选D.



科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,进价为每个20元,规定每个商品售价不低于进价,且不高于60元,经调查发现,每天的销售量y(个)与每个商品的售价x(元)满足一次函数关系,其部分数据如下所示:
每个商品的售价x(元) | … | 30 | 40 | 50 | … |
每天的销售量y(个) | 100 | 80 | 60 | … |
(1)求y与x之间的函数表达式;
(2)设商场每天获得的总利润为w(元),求w与x之间的函数表达式;
(3)不考虑其他因素,当商品的售价为多少元时,商场每天获得的总利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的内心为I,外心为O
(1)试找出∠A与∠BOC,∠A与∠BIC的数量关系
(2)由(1)题的结论写出∠BOC与∠BIC的关系

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC于E点,连接DE交OC于F点,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
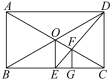
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AD=2AG;②GE:BE=1:3;③![]() ,其中正确的是( )
,其中正确的是( )

A. ①② B. ①②③ C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电视塔AB和楼CD的水平距离为100 m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为__________,楼高为__________.
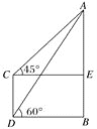
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的售价p(元/千克)与时间t(天)之间的函数表达式为
p=
且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求第30天的日销售量是多少?
(2)问:哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com