
分析 (1)根据a1+a2=0,b1=b2,c1+c2=0,求出a2=-1,b2=-3,c2=-2,从而求出函数y=x2-3x-2的“旋转函数”;
(2)根据旋转函数的定义得到:$\left\{\begin{array}{l}{\frac{3}{5}m=-3n}\\{-3+n=0}\end{array}\right.$,从而解得m=-15,n=3,进而求出$(\frac{4}{15}m+n{)^{2015}}$的值;
(3)根据题意写出抛物线L的“旋转函数”解析式,然后把点(-m,-n)代入进行验证即可;
(4)根据题意得A(-1,0),B(4,0),C(0,2),得到A1(1,0),B1(-4,0),C1(0,-2),从而求出两个函数解析式,进而得到两个函数互为“旋转函数”.
解答 解:(1)在y=-x2+4x-3中,a1=-1,b1=4,c1=-3,
∵a1+a2=0,b1=b2,c1+c2=0,
∴a2=1,b2=4,c2=3,
可得函数y=-x2+4x-3的“旋转函数”为y=x2+4x+3;
(2)根据题意得$\left\{\begin{array}{l}{\frac{3}{5}m=-3n}\\{-3+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-15}\\{n=3}\end{array}\right.$.
$(\frac{4}{15}m+n{)^{2015}}$=[$\frac{4}{15}$×(-15)+3]2015=-1;
(3)证明:点A关于原点对称的点为A′,则点A(m,n)关于原点对称的点的坐标为A′(-m,-n).
抛物线Ly=ax2+bx+c的“旋转函数”解析式为y=-ax2+bx-c.
把点A′(-m,-n)代入得到:-n=-a(-m)2-mb-c=-am2-mb-c,则n=am2+bm+c,即点(m,n)在抛物线y=ax2+bx+c上,
所以点A关于原点的对称点在抛物线L的“旋转函数”上.
(4)题意得A(-1,0),B(4,0),C(0,2),得到A1(1,0),B1(-4,0),C1(0,-2),
又∵y=-$\frac{1}{2}$(x+1)(x-4)即y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2,经过点A1,B1,C1的二次函数为y=$\frac{1}{2}$(x-1)(x+4)=$\frac{1}{2}$x2+$\frac{3}{2}$x-2,
∵a1+a2=0,b1=b2,c1+c2=0,
∴两个函数互为“旋转函数”.
点评 本题考查了二次函数的综合题:熟练掌握关于原点对称的两点的坐标特征;会求二次函数图象与坐标轴的交点和待定系数法求二次函数解析式;对新定义的理解能力.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源:2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷(解析版) 题型:填空题
比较下列各数的大小: 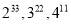 ; ____________________
; ____________________
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
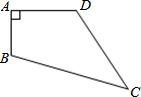 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积36cm2.
已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,则四边形ABCD的面积36cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com