
【题目】如图,在△ABC中,以AB为直径的⊙O交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,且DH是⊙O的切线,连接DE交AB于点F.
(1)求证:DC=DE;
(2)若AE=1,![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)见解析;(2)![]() .
.
【解析】
(1)连接OD,由DH⊥AC,DH是⊙O的切线,然后由平行线的判定与性质可证∠C=∠ODB,由圆周角定理可得∠OBD=∠DEC,进而∠C=∠DEC,可证结论成立;
(2)证明△OFD∽△AFE,根据相似三角形的性质即可求出圆的半径.
(1)证明:连接OD,
由题意得:DH⊥AC,由且DH是⊙O的切线,∠ODH=∠DHA=90°,
∴∠ODH=∠DHA=90°,
∴OD∥CA,
∴∠C=∠ODB,
∵OD=OB,
∴∠OBD=∠ODB,
∴∠OBD=∠C,
∵∠OBD=∠DEC,
∴∠C=∠DEC,
∴DC=DE;
(2)解:由(1)可知:OD∥AC,
∴∠ODF=∠AEF,
∵∠OFD=∠AFE,
∴△OFD∽△AFE,
∴![]() ,
,
∵AE=1,
∴OD=![]() ,
,
∴⊙O的半径为![]() .
.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
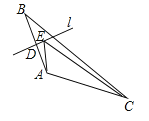
【题目】如图,在△ABC中,点D是AB边的中点,过点D作边AB的垂线l,E是l上任意一点,且AC=5,BC=8,则△AEC的周长最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
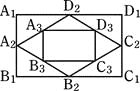
【题目】如图,矩形A1B1C1D1的面积为4,顺次连结各边中点得到四边形A2B2C2D2,再顺次连结四边形A2B2C2D2四边中点得到四边形A3B3C3D3,依此类推,则四边形AnBnCnDn的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将每件进价为80元的某种商店按每件110元出售,每天可售出100件.该商店想通过降低售价、增加销售量的方法来提高利润.经市场调查,发现这种商品每件每降价5元,每天的销售量可增加50件.设商品降价x元,每天销售该商品获得的利润为y元.
(1)求y(元)关于x(元)的函数关系式,并写出x的取值范围.
(2)求当x取何值时y最大?并求出y的最大值.
(3)若要是每天销售利润为3750元,且尽可能最大的向顾客让利,应将该商品降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往距离单位10km的培训中心参加学习,图中1,![]() 分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )
分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象,以下说法:①甲比乙提前12分钟到达;②甲的平均速度为15千米/小时;③甲、乙相遇时,乙走了6千米;④乙出发6分钟后追上甲,其中正确的是( )
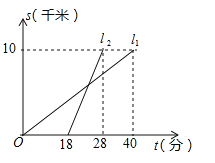
A.①②B.③④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
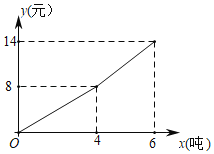
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水4吨以内(包括4吨)和用水4吨以上收费标准(收费标准:每吨水的价格)某用户每月应交水费y(元)与用水量x(吨)之间关系的图象如图:
(1)说出自来水公司在这两个用水范围内的收费标准;
(2)当x>4时,求因变量y与自变量x之间的关系式;
(3)若某用户该月交水费26元,求他用了多少吨水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com