
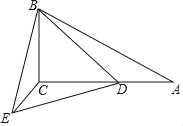
【题目】在Rt△ABC中,∠A=30°,∠ACB=90°,AB=10,D为AC上点.将BD绕点B顺时针旋转60°得到BE,连接CE.
(1)证明:∠ABD=∠CBE;
(2)连接ED,若ED=2![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据三角形的内角和得到∠ABC=60°,根据旋转的性质得到∠EBD=60°,根据角的和差即可得到∠ABD=∠CBE;
(2)过D作DH⊥AB于H,解直角三角形得到AD=2DH,AH=![]() DH,求得BH=10﹣
DH,求得BH=10﹣![]() DH,推出△BDE是等边三角形,得到BD=DE=2
DH,推出△BDE是等边三角形,得到BD=DE=2![]() ,根据勾股定理列方程即可得到结论.
,根据勾股定理列方程即可得到结论.
(1)∵在Rt△ABC中,∠A=30°,∠ACB=90°,
∴∠ABC=60°,
∵将BD绕点B顺时针旋转60°得到BE,
∴∠EBD=60°,
∴∠ABD=60°﹣∠CBD,∠CBE=60°﹣∠CBD,
∴∠ABD=∠CBE;
(2)过D作DH⊥AB于H,
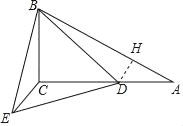
∵∠A=30°,
∴AD=2DH,AH=![]() DH,
DH,
∴BH=10﹣![]() DH,
DH,
∵将BD绕点B顺时针旋转60°得到BE,
∴BE=BD,
∴△BDE是等边三角形,
∴BD=DE=2![]() ,
,
在Rt△BDH中,BD2=BH2+DH2,
即(2![]() )2=(10﹣
)2=(10﹣![]() DH)2+DH2,
DH)2+DH2,
解得:DH=![]() ,或DH=4
,或DH=4![]() (不合题意舍去),
(不合题意舍去),
∴AD=2![]() ,
,
∵AC=5![]() ,
,
∴CD=3![]() ,
,
∴![]() =
=![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】将一条长为56cm的铁丝剪成两段并把每一段铁丝做成一个正方形.
(1)要使这两个正方形的面积之和等于100cm2,该怎么剪?
(2)设这两个正方形的面积之和为Scm2,当两段铁丝长度分别为何值时,S有最小值?
查看答案和解析>>
科目:初中数学 来源: 题型:
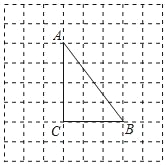
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.(1)计算AB的长等于__,(2)请在如图所示的网格中,用无刻度的直尺,画出一个△ADE,使△ADE~△ABC,且满足点D在AC边上,点E在AB边上,AE=2.简要说明画图方法(不要求证明)__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中有一格点三角形,该三角形的三个顶点为:A(1,1)、B(﹣3,1)、C(﹣3.﹣1)
(1)若△ABC的外接圆的圆心为P,则点P的坐标为_____.
(2)如图所示,在11×8的网格图内,以坐标原点O点为位似中心,将△ABC按相似比2:1放大,A、B、C的对应点分别为A′、B′、C′,得到△A′B′C′,在图中画出△A′B′C′;若将△A′B′C′沿x轴方向平移,需平移_____单位长度,能使得B′C′所在的直线与⊙P相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
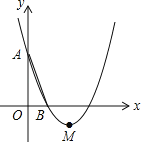
【题目】如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(1)求b、c的值;
(2)若只沿y轴上下平移该抛物线后与y轴的交点为A1,顶点为M1,且四边形AMM1A1是菱形,写出平移后抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,2)与(0,3)之间(不包括这两点),对称轴为直线x=2.下列结论:abc<0;②9a+3b+c>0;③若点M(![]() ,y1),点N(
,y1),点N(![]() ,y2)是函数图象上的两点,则y1<y2;④﹣
,y2)是函数图象上的两点,则y1<y2;④﹣![]() <a<﹣
<a<﹣![]() .其中正确结论有( )
.其中正确结论有( )
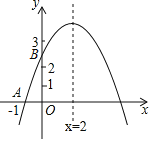
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
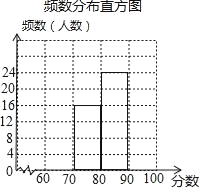
【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
分数段 | 频数(人数) |
60≤x<70 | a |
70≤x<80 | 16 |
80≤x<90 | 24 |
90≤x<100 | b |
请解答下列问题:
(1)完成频数分布表,a= ,b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
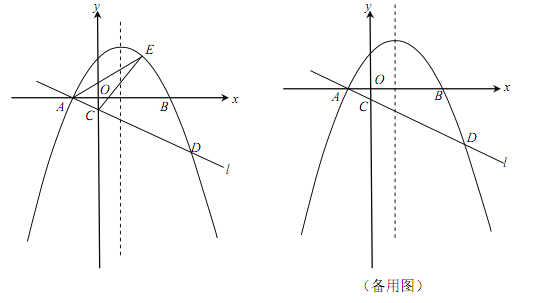
【题目】(本小题满分12分)如图,在平面直角坐标系xOy中,抛物线![]() (
(![]() )与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:
)与x轴交于A,B两点(点A在点B的左侧),经过点A的直线l:![]() 与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.
(1)直接写出点A的坐标,并求直线l的函数表达式(其中k,b用含a的式子表示);
(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为![]() ,求a的值;
,求a的值;
(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A,D,P,Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com