
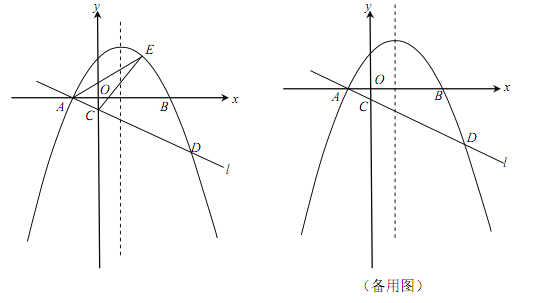
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж12ЗжЃЉШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯп![]() ЃЈ
ЃЈ![]() ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌОЙ§ЕуAЕФжБЯпlЃК
ЃЉгыxжсНЛгкAЃЌBСНЕуЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌОЙ§ЕуAЕФжБЯпlЃК![]() гыyжсИКАыжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЌЧвCD=4ACЃЎ
гыyжсИКАыжсНЛгкЕуCЃЌгыХзЮяЯпЕФСэвЛИіНЛЕуЮЊDЃЌЧвCD=4ACЃЎ
ЃЈ1ЃЉжБНгаДГіЕуAЕФзјБъЃЌВЂЧѓжБЯпlЕФКЏЪ§БэДяЪНЃЈЦфжаkЃЌbгУКЌaЕФЪНзгБэЪОЃЉЃЛ
ЃЈ2ЃЉЕуEЪЧжБЯпlЩЯЗНЕФХзЮяЯпЩЯЕФЖЏЕуЃЌШєЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЧѓaЕФжЕЃЛ
ЃЌЧѓaЕФжЕЃЛ
ЃЈ3ЃЉЩшPЪЧХзЮяЯпЕФЖдГЦжсЩЯЕФвЛЕуЃЌЕуQдкХзЮяЯпЩЯЃЌвдЕуAЃЌDЃЌPЃЌQЮЊЖЅЕуЕФЫФБпаЮФмЗёГЩЮЊОиаЮЃПШєФмЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈЃ1ЃЌ0ЃЉЃЌ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉPЕФзјБъЮЊЃЈ1ЃЌ
ЃЛЃЈ3ЃЉPЕФзјБъЮЊЃЈ1ЃЌ![]() ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉдк![]() жаЃЌСюy=0ЃЌЕУЕН
жаЃЌСюy=0ЃЌЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌЕУЕНAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгЩжБЯпlОЙ§ЕуAЃЌЕУЕН
ЃЌЕУЕНAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌгЩжБЯпlОЙ§ЕуAЃЌЕУЕН![]() ЃЌЙЪ
ЃЌЙЪ![]() ЃЌСю
ЃЌСю![]() ЃЌМД
ЃЌМД![]() ЃЌгЩгкCDЃН4ACЃЌЙЪЕуDЕФКсзјБъЮЊ4ЃЌМДга
ЃЌгЩгкCDЃН4ACЃЌЙЪЕуDЕФКсзјБъЮЊ4ЃЌМДга![]() ЃЌЕУЕН
ЃЌЕУЕН![]() ЃЌДгЖјЕУГіжБЯпlЕФКЏЪ§БэДяЪНЃЛ
ЃЌДгЖјЕУГіжБЯпlЕФКЏЪ§БэДяЪНЃЛ
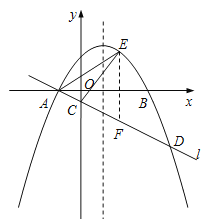
ЃЈ2ЃЉЙ§ЕуEзїEFЁЮyжсЃЌНЛжБЯпlгкЕуFЃЌЩшEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђFЃЈ
ЃЉЃЌдђFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
EFЃН![]() =
=![]() ЃЌSЁїACEЃНSЁїAFEЃSЁїCFEЃН
ЃЌSЁїACEЃНSЁїAFEЃSЁїCFEЃН![]() ЃН
ЃН![]() ЃЌЙЪЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЙЪЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЖјЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЖјЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСю![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЕУЕНDЃЈ4ЃЌ5aЃЉЃЌвђЮЊХзЮяЯпЕФЖдГЦжсЮЊ
ЃЌЕУЕНDЃЈ4ЃЌ5aЃЉЃЌвђЮЊХзЮяЯпЕФЖдГЦжсЮЊ![]() ЃЌЩшPЃЈ1ЃЌmЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЃКЂйШєADЪЧОиаЮЕФвЛЬѕБпЃЌЂкШєADЪЧОиаЮЕФвЛЬѕЖдНЧЯпЃЎ
ЃЌЩшPЃЈ1ЃЌmЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЃКЂйШєADЪЧОиаЮЕФвЛЬѕБпЃЌЂкШєADЪЧОиаЮЕФвЛЬѕЖдНЧЯпЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп![]() =
=![]() ЃЌСюy=0ЃЌЕУЕН
ЃЌСюy=0ЃЌЕУЕН![]() ЃЌ
ЃЌ![]() ЃЌЁрAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЁпжБЯпlОЙ§ЕуAЃЌЁр
ЃЌЁрAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌЁпжБЯпlОЙ§ЕуAЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]() ЃЌСю
ЃЌСю![]() ЃЌМД
ЃЌМД![]() ЃЌЁпCDЃН4ACЃЌЁрЕуDЕФКсзјБъЮЊ4ЃЌЁр
ЃЌЁпCDЃН4ACЃЌЁрЕуDЕФКсзјБъЮЊ4ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁржБЯпlЕФКЏЪ§БэДяЪНЮЊ
ЃЌЁржБЯпlЕФКЏЪ§БэДяЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЙ§ЕуEзїEFЁЮyжсЃЌНЛжБЯпlгкЕуFЃЌЩшEЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђFЃЈ
ЃЉЃЌдђFЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
EFЃН![]() =
=![]() ЃЌ
ЃЌ
SЁїACEЃНSЁїAFEЃSЁїCFEЃН![]()
ЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЁпЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ
ЃЌЁпЁїACEЕФУцЛ§ЕФзюДѓжЕЮЊ![]() ЃЌЁр
ЃЌЁр![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСю![]() ЃЌМД
ЃЌМД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ![]() ЃЌЁрDЃЈ4ЃЌ5aЃЉЃЌЁп
ЃЌЁрDЃЈ4ЃЌ5aЃЉЃЌЁп![]() ЃЌЁрХзЮяЯпЕФЖдГЦжсЮЊ
ЃЌЁрХзЮяЯпЕФЖдГЦжсЮЊ![]() ЃЌЩшPЃЈ1ЃЌmЃЉЃЌ
ЃЌЩшPЃЈ1ЃЌmЃЉЃЌ
ЂйШєADЪЧОиаЮЕФвЛЬѕБпЃЌдђQЃЈЃ4ЃЌ21aЃЉЃЌmЃН21aЃЋ5aЃН26aЃЌдђPЃЈ1ЃЌ26aЃЉЃЌЁпЫФБпаЮADPQЮЊОиаЮЃЌЁрЁЯADPЃН90ЁуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌЁп
ЃЌЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁрP1ЃЈ1ЃЌ
ЃЌЁрP1ЃЈ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
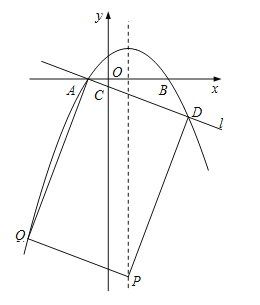
ЂкШєADЪЧОиаЮЕФвЛЬѕЖдНЧЯпЃЌдђЯпЖЮADЕФжаЕузјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌQЃЈ2ЃЌ
ЃЉЃЌQЃЈ2ЃЌ![]() ЃЉЃЌmЃН
ЃЉЃЌmЃН![]() ЃЌдђPЃЈ1ЃЌ8aЃЉЃЌЁпЫФБпаЮAPDQЮЊОиаЮЃЌЁрЁЯAPDЃН90ЁуЃЌЁр
ЃЌдђPЃЈ1ЃЌ8aЃЉЃЌЁпЫФБпаЮAPDQЮЊОиаЮЃЌЁрЁЯAPDЃН90ЁуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌМД
ЃЌМД![]() ЃЌЁп
ЃЌЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁрP2ЃЈ1ЃЌЃ4ЃЉЃЎ
ЃЌЁрP2ЃЈ1ЃЌЃ4ЃЉЃЎ
злЩЯЫљЪіЃЌвдЕуAЁЂDЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮФмГЩЮЊОиаЮЃЌЕуPЕФзјБъЮЊЃЈ1ЃЌ![]() ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
ЃЉЛђЃЈ1ЃЌЃ4ЃЉЃЎ
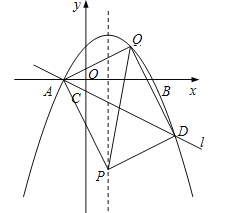



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
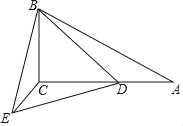
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯAЃН30ЁуЃЌЁЯACBЃН90ЁуЃЌABЃН10ЃЌDЮЊACЩЯЕуЃЎНЋBDШЦЕуBЫГЪБеыа§зЊ60ЁуЕУЕНBEЃЌСЌНгCEЃЎ
ЃЈ1ЃЉжЄУїЃКЁЯABDЃНЁЯCBEЃЛ
ЃЈ2ЃЉСЌНгEDЃЌШєEDЃН2![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЧјЮЊСЫДДНЈЙњМвМЖЮРЩњГЧЧјЃЌЖдЯНЧјФквЛаЉХЉУГЪаГЁашвЊДІРэЃЌДІРэЕФЗНЪНгаСНжжЃЌвЛжжЪЧВЛИФБфЕиРэЮЛжУОЭЕиИФдьЃЛСэвЛжжЪЧИФБфЕиРэЮЛжУЃЌбЁдёвЛИіКЯРэЕФЮЛжУжиаТНЈХЉУГЪаГЁ.ОЕїбаЃЌашвЊДІРэЕФХЉУГЪаГЁЙВга300ЭђЦНЗНУзЃЌИУЧјИљОнЧјЧщЃЌЯоЖЈОЭЕиИФдьЕФУцЛ§ВЛЕУЩйгкаТНЈУцЛ§ЕФ2БЖ.
ЃЈ1ЃЉаТНЈХЉУГЪаГЁЕФУцЛ§зюЖрЪЧЖрЩйЭђЦНЗНУзЃП
ЃЈ2ЃЉИУЧјМЦЛЎвдУПЦНЗНУз4000дЊЕФдьМлаоНЈЃЈ1ЃЉжааТНЈУцЛ§зюЖрЕФХЉУГЪаГЁЃЌвдУПЦНЗНУз1000дЊЕФдьМлИФдьЦфЫќашвЊОЭЕиДІРэЕФХЉУГЪаГЁ.ЕЋдкЪЕМЪЪЉЙЄжаЃЌаТНЈЕФХЉУГЪаГЁУцЛ§діМгСЫ![]() ЃЌУПЦНЗНУзЕФдьМлЯТНЕСЫ
ЃЌУПЦНЗНУзЕФдьМлЯТНЕСЫ![]() ЃЌОЭЕиИФдьЕФХЉУГЪаГЁЕФУцЛ§УЛгаБфЃЌЕЋУПЦНЗНУзЕФдьМлЯТНЕСЫ
ЃЌОЭЕиИФдьЕФХЉУГЪаГЁЕФУцЛ§УЛгаБфЃЌЕЋУПЦНЗНУзЕФдьМлЯТНЕСЫ![]() ЃЌНсЙћзмЗбгУгыМЦЛЎГжЦНЃЌЧѓ
ЃЌНсЙћзмЗбгУгыМЦЛЎГжЦНЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПга5еХе§УцЗжБ№аДгаЪ§зжЉ1ЃЌ-![]() ЃЌ0ЃЌ1ЃЌ3ЕФПЈЦЌЃЌЫќУЧГ§Ъ§зжВЛЭЌЭтШЋВПЯрЭЌЃЎНЋЫќУЧБГУцГЏЩЯЃЌЯДдШКѓДгжаЫцЛњЕФГщШЁвЛеХЃЌМЧПЈЦЌЩЯЕФЪ§зжЮЊaЃЌдђЪЙвдxЮЊздБфСПЕФЗДБШР§КЏЪ§
ЃЌ0ЃЌ1ЃЌ3ЕФПЈЦЌЃЌЫќУЧГ§Ъ§зжВЛЭЌЭтШЋВПЯрЭЌЃЎНЋЫќУЧБГУцГЏЩЯЃЌЯДдШКѓДгжаЫцЛњЕФГщШЁвЛеХЃЌМЧПЈЦЌЩЯЕФЪ§зжЮЊaЃЌдђЪЙвдxЮЊздБфСПЕФЗДБШР§КЏЪ§![]() ОЙ§ЖўЁЂЫФЯѓЯоЃЌЧвЙигкxЕФЗНГЬ
ОЙ§ЖўЁЂЫФЯѓЯоЃЌЧвЙигкxЕФЗНГЬ![]() гаЪЕЪ§НтЕФИХТЪЪЧ_____ЃЎ
гаЪЕЪ§НтЕФИХТЪЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
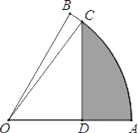
ЁОЬтФПЁПШчЭМЃЌЩШаЮOABжаЃЌЁЯAOB=60ЁуЃЌЩШаЮАыОЖЮЊ4ЃЌЕуCдк![]() ЩЯЃЌCDЁЭOAЃЌДЙзуЮЊЕуDЃЌЕБЁїOCDЕФУцЛ§зюДѓЪБЃЌЭМжавѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ
ЩЯЃЌCDЁЭOAЃЌДЙзуЮЊЕуDЃЌЕБЁїOCDЕФУцЛ§зюДѓЪБЃЌЭМжавѕгАВПЗжЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛжжЦЗХЦг№ШоЗўКЭЗРКЎЗўЃЌЦфжаг№ШоЗўЕФЪлМлЪЧЗРКЎЗўЪлМлЕФ5БЖЛЙЖр100дЊЃЌ2014Фъ1дТЗнЃЈДКНкЧАЦкЃЉЙВЯњЪл500МўЃЌг№ШоЗўгыЗРКЎЗўЯњСПжЎБШЪЧ4ЃК1ЃЌЯњЪлзмЪеШыЮЊ58.6ЭђдЊЃЎ
ЃЈ1ЃЉЧѓг№ШоЗўКЭЗРКЎЗўЕФЪлМлЃЛ
ЃЈ2ЃЉДКНкКѓЯњЪлНјШыЕМОЃЌ2014Фъ2дТЗнг№ШоЗўЯњСПЯТЛЌСЫ6m%ЃЌЪлМлЯТЛЌСЫ4m%ЃЌЗРКЎЗўЯњСПКЭЪлМлЖМЮЌГжВЛБфЃЌНсЙћЯњЪлзмЪеШыЯТНЕЮЊ16.04ЭђдЊЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
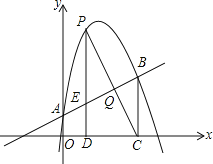
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+1ОЙ§ЕуЃЈ2ЃЌ6ЃЉЃЌЧвгыжБЯпy=![]() x+1ЯрНЛгкAЃЌBСНЕуЃЌЕуAдкyжсЩЯЃЌЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊЕуCЃЈ4ЃЌ0ЃЉЃЎ
x+1ЯрНЛгкAЃЌBСНЕуЃЌЕуAдкyжсЩЯЃЌЙ§ЕуBзїBCЁЭxжсЃЌДЙзуЮЊЕуCЃЈ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєPЪЧжБЯпABЩЯЗНИУХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЌНЛABгкЕуEЃЌЧѓЯпЖЮPEЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЃЌЩшPCгыABЯрНЛгкЕуQЃЌЕБЯпЖЮPCгыBEЯрЛЅЦНЗжЪБЃЌЧыЧѓГіЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃПЊеЙбабЇТУааЛюЖЏЃЌзМБИШЅЕФбабЇЛљЕигаAЃЈЧњИЗЃЉЁЂBЃЈСКЩНЃЉЁЂCЃЈуыЩЯЃЉЃЌDЃЈуєЫЎЃЉЃЌУПЮЛбЇЩњжЛФмбЁШЅвЛИіЕиЗНЃЌЭѕРЯЪІЖдБОШЋЬхЭЌбЇбЁШЁЕФбабЇЛљЕиЧщПіНјааЕїВщЭГМЦЃЌЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЈШчЭМЫљЪОЃЉЃЎ
ЃЈ1ЃЉЧѓИУАрЕФзмШыЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЎ
ЃЈ2ЃЉЧѓDЃЈуєЫЎЃЉЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЃЛ
ЃЈ3ЃЉИУАрАрЮЏ4ШЫжаЃЌ1ШЫбЁШЅЧњИЗЃЌ2ШЫбЁШЅСКЩНЃЌ1ШЫбЁШЅуыЩЯЃЌЭѕРЯЪІвЊДгет4ШЫжаЫцЛњГщШЁ2ШЫСЫНтЫћУЧЖдбабЇЛљЕиЕФПДЗЈЃЌЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЫљГщШЁЕФ2ШЫжаЧЁКУга1ШЫбЁШЅЧњИЗЃЌ1ШЫбЁШЅСКЩНЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌBDЮЊдВOЕФжБОЖЃЌжБЯпEDЮЊдВOЕФЧаЯпЃЌAЁЂCСНЕудкдВЩЯЃЌACЦНЗжЁЯBADЧвНЛBDгкFЕуЃЎШєЁЯADEЃН19ЁуЃЌдђЁЯAFBЕФЖШЪ§ЮЊКЮЃП(ЁЁЁЁ)
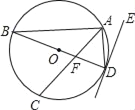
A. 97Ёу B. 104Ёу C. 116Ёу D. 142Ёу
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com