练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，BD为圆O的直径，直线ED为圆O的切线，A、C两点在圆上，AC平分∠BAD且交BD于F点．若∠ADE＝19°，则∠AFB的度数为何？(　　)

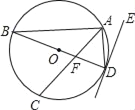
    A. 97° B. 104° C. 116° D. 142°

    【答案】C

    【解析】

    先根据直径所对的圆周角为直角得出∠BAD的度数，根据角平分线的定义得出∠BAF的度数，再根据弦切角等于它所夹弧对的圆周角，得出∠ABD的度数，最后利用三角形内角和定理即可求出∠AFB的度数．

    ∵BD是圆O的直径，
    ∴∠BAD=90°，
    又∵AC平分∠BAD，
    ∴∠BAF=∠DAF=45°，
    ∵直线ED为圆O的切线，
    ∴∠ADE=∠ABD=19°，
    ∴∠AFB=180°-∠BAF-∠ABD=180°-45°-19°=116°．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

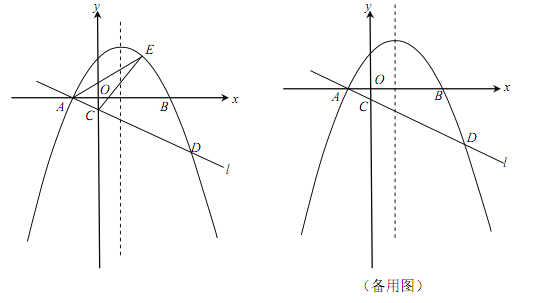
    【题目】（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线（）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．

    （1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；

    （2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为，求a的值；

    （3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

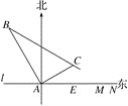
    【题目】在某飞机场东西方向的地面l上有一长为1 km的飞机跑道MN(如图)，在跑道MN的正西端14.5千米处有一观察站A.某时刻测得一架匀速直线降落的飞机位于点A的北偏西30°，且与点A相距15千米的B处；经过1分钟，又测得该飞机位于点A的北偏东60°，且与点A相距5千米的C处．

    (1)该飞机航行的速度是多少千米/小时？(结果保留根号)

    (2)如果该飞机不改变航向继续航行，那么飞机能否降落在跑道MN之间？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于x的方程mx2﹣x﹣m+1＝0，有以下三个结论：

    ①当m＝0时，方程只有一个实数解；

    ②当m≠0时，方程有两个不相等的实数解；

    ③无论m取何值，方程都有一个整数根．

    (1)请你判断，这三个结论中正确的有_____(填序号)

    (2)证明(1)中你认为正确的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△AOB中，∠O＝90°，AO＝18cm，BO＝30cm，动点M从点A开始沿边AO以1cm/s的速度向终点O移动，动点N从点O开始沿边OB以2cm/s的速度向终点B移动，一个点到达终点时，另一个点也停止运动．如果M、N两点分别从A、O两点同时出发，设运动时间为ts时四边形ABNM的面积为Scm2．

    (1)求S关于t的函数关系式，并直接写出t的取值范围；

    (2)判断S有最大值还是有最小值，用配方法求出这个值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

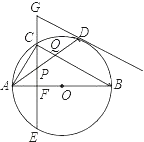
    【题目】如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是的中点，弦CE⊥AB于点F，过点D的切线交EC的延长线于点G，连接AD，分别交CF、BC于点P、Q，连接AC．给出下列结论：①∠BAD＝∠ABC；②GP＝GD；③点P是△ACQ的外心；④APAD＝CQCB．其中正确的是_____（写出所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，二次函数y＝x2﹣2x﹣3的图象与x轴交于A、B两点，与y轴交于点C，则下列说法错误的是（　　）

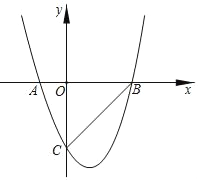
    A. AB＝4

    B. ∠ABC＝45°

    C. 当x＞0时，y＜﹣3

    D. 当x＞1时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠B=90°，AB=12，BC=24，动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动，动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动，如果点P、Q分别从点A、B同时出发，那么△PBQ的面积S随出发时间t（s）如何变化？写出函数关系式及t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是置于水平地面上的一个球形储油罐，小敏想测量它的半径、在阳光下，他测得球的影子的最远点A到球罐与地面接触点B的距离是10米(如示意图，AB＝10米)；同一时刻，他又测得竖直立在地面上长为1米的竹竿的影子长为2米，那么，球的半径是________米．

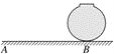
    查看答案和解析>>

    同步练习册答案