

分析 (1)只要证明∠ACP=∠BCP,即可根据SAS证明;
(2)分三种情形①BQ=QD.②BQ=BD.③BD=DQ即可解决问题;
解答 (1)证明:∵△ABC和△PQC是等边三角形,
∴AC=BC,PC=QC,∠ACB=∠PCQ=60°,
又∵∠ACP=60°-∠BCP,∠BCQ=60°-∠BCP,
∴∠ACP=∠BCP,
在△ACP和△BCQ中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCQ}\\{PC=QC}\end{array}\right.$,
∴△ACP≌△BCQ(SAS).
(2)解:由(1)知,△ACP≌△BCQ,∴∠QBD=∠PAC=30°,
当△BDQ 是等腰三角形时,
①若BQ=QD,如图1,则∠BDQ=30°; 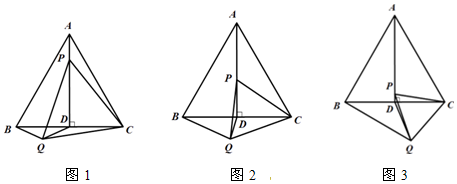
②若BQ=BD,如图2,则∠BDQ=75°;
③若BD=DQ,如图3,则∠BDQ=120°.
点评 本题考查全等三角形的判定和性质、等边三角形的性质和判定等知识,解题的关键是正确寻找全等三角形解决问题学会用分类讨论的思想思考问题,属于中考常考题型.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小王参加本次数学考试,成绩是150分 | |
| B. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| C. | 某设计运动射靶一次,正中靶心 | |
| D. | 口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
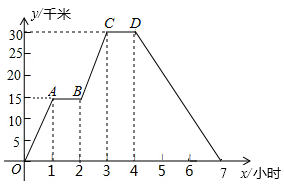 小明同学骑自行车沿平直路线行进,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.
小明同学骑自行车沿平直路线行进,下图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
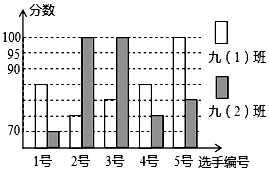 为了弘扬“中国梦”,某校初三(1)班和(2)班各5名学生参加以“诚信友善”为主题的演讲比赛活动,根据他们的得分情况绘制如下的统计图:
为了弘扬“中国梦”,某校初三(1)班和(2)班各5名学生参加以“诚信友善”为主题的演讲比赛活动,根据他们的得分情况绘制如下的统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).
如图所示,△ABC在平面直角坐标系中,A,B,C的坐标分别是A(-3,3),B(-5,-1),C(-1,1); 点P(m,n)是△ABC内部的一点,平移△ABC,点A、B、C、P的对应点分别是A'、B'、C'、P'.且点P'的坐标为(m+4,n-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com