
【题目】在平面直角坐标系中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=![]() ,则称点Q为点P的“亲密点”.即:当x≥0时,点P(x,y)的“亲密点”Q的坐标为(x,y+1);当x<0时,点P(x,y)的“亲密点”Q的坐标为(x,-y).例如:点(1,2)的“亲密点”为点(1,3),点(-1,3)的“亲密点”为点(-1,-3).
,则称点Q为点P的“亲密点”.即:当x≥0时,点P(x,y)的“亲密点”Q的坐标为(x,y+1);当x<0时,点P(x,y)的“亲密点”Q的坐标为(x,-y).例如:点(1,2)的“亲密点”为点(1,3),点(-1,3)的“亲密点”为点(-1,-3).
(1)点(2,-3)的“亲密点”为______;______的“亲密点”是(-2,-5).
(2)点M(m+1,5)是一次函数y=x+3图象上点N的“亲密点”,求点N的坐标.
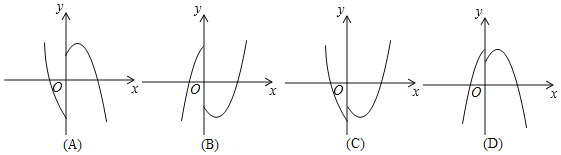
(3)若点P在函数y=x2-2x-3的图象上.则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是______.
(4)若点P在二次函数y=x2-2x-5的图象上,当-2<x≤a时,其亲密点Q的纵坐标y′满足-5≤y′≤5,请直接写出a的取值范围.
【答案】(1)(2,-2),(-2,5);(2)N1(1,4),N2(-2,-5);(3)B;(4)1≤a≤1+![]()
【解析】
(1)根据“亲密点”的定义即可求得;(2)分两种情况进行讨论:当m+1≥0时,点M的纵坐标为5,令5=y+1,则y=4,把y=4代入y=x+3求得x的值,即M(1,4);当m+1<0时,点M的纵坐标为-5,代入y=x+3求得x的值,即M(-2,-5);(3)根据函数y=x2-2x-3的图象,依据“亲密点”的定义找出y′关于x的函数图象,由此即可得出结论;(4)根据“亲密点”的定义,可得函数解析式,根据自变量与函数值得对应关系,可得答案.
(1)点(2,-3)的“亲密点”为(2,-2),(-2,5)的“亲密点”是(-2,-5).
故答案为(2,-2),(-2,5);
(2)N1(1,4),N2(-2,-5),
(3)由函数y=x2-2x-3=(x-3)(x+1)可知:抛物线开口向上,与x轴有两个交点,交y轴与负半轴,所以将y轴左侧的图象关于x轴颠倒过来,将y轴右侧的图象向上平移1个单位,即可得出y′关于x的函数图象.
故选B;
(4)由题意,得
y=x2-2x-5的图象上的点P的亲密点Q必在函数
y′=![]() 的图象上,
的图象上,
当x=-2时,-x2+2x+5=5,
∵y′=-x2+2x+5>-5(x<0),
∴y′=-5在y′=x2-2x-4(x≥0)上,y′=5在y′=x2-2x-4(x≥0)上,
∴-5=x2-2x-4,
解得x=1,
∴5=x2-2x-4,
解得x=1+![]() ,x=1-
,x=1-![]() (舍去),
(舍去),
∴1≤a≤1+![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1.△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC作等腰Rt△ABE和等腰Rt△ACF,过点E,F作射线GA的垂线,垂足分别为P,Q.
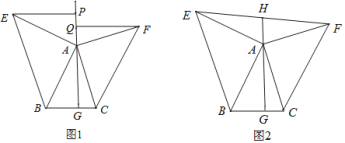
(1)求证:△EPA≌△AGB:
(2)试探究EP与FQ之间的数量关系,并证明你的结论;
(3)如图2.若连接EF交GA的延长线于H,由(2)中的结论你能判断EH与FH的大小关系吗?并说明理由:
(4)在(3)的条件下,若BC=10,AG=12.请直接写出S△AEF= .
查看答案和解析>>
科目:初中数学 来源: 题型:
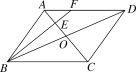
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
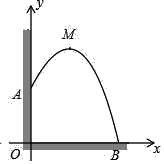
【题目】从某幢建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与地面垂直).抛物线的最高点M离墙1m,离地面![]() m.
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式.
(2)求水的落地点B与点O的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
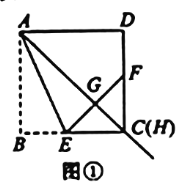
【题目】在正方形![]() 中,过点A引射线
中,过点A引射线![]() ,交边
,交边![]() 于点H(H不与点D重合).通过翻折,使点B落在射线
于点H(H不与点D重合).通过翻折,使点B落在射线![]() 上的点G处,折痕
上的点G处,折痕![]() 交
交![]() 于E,连接E,G并延长
于E,连接E,G并延长![]() 交
交![]() 于F.
于F.
(1)如图1,当点H与点C重合时,![]() 与
与![]() 的大小关系是_________;
的大小关系是_________;![]() 是____________三角形.
是____________三角形.
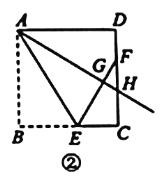
(2)如图2,当点H为边![]() 上任意一点时(点H与点C不重合).连接
上任意一点时(点H与点C不重合).连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
(3)在图2,当![]() ,
,![]() 时,求
时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新华商场销售某种冰箱,每台进价为2500元,销售价为2900元,平均每天能售出8台;调查发现,当销售价每降低50元,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱应该降价多少元?若设每台冰箱降价x元,根据题意可列方程( )
A. (2900-x)(8+4×![]() )=5000 B. (400-x)(8+4×
)=5000 B. (400-x)(8+4×![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com