
【题目】一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种B.1种C.2种D.3种
【答案】B
【解析】
先判断出两根铝材哪根为边,需截哪根,再根据相似三角形的对应边成比例求出另外两边的长,由另外两边的长的和与另一根铝材相比较即可.
∵两根铝材的长分别为27cm、45cm,若45cm为一边时,
则另两边的和为27cm,27<45,不能构成三角形,
∴必须以27cm为一边,45cm的铝材为另外两边,
设另外两边长分别为x、y,则
(1)若27cm与24cm相对应时,
![]() ,
,
解得:x=33.75cm,y=40.5cm,
x+y=33.75+40.5=74.25cm>45cm,故不成立;
(2)若27cm与36cm相对应时,
![]() ,
,
解得:x=22.5cm,y=18cm,x+y=22.5+18=40.5cm<45cm,成立;
(3)若27cm与30cm相对应时,
![]() ,
,
解得:x=32.4cm,y=21.6cm,x+y=32.4+21.6=54cm>45cm,故不成立;
故只有一种截法.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是直径AB所对的半圆弧,点C在
是直径AB所对的半圆弧,点C在![]() 上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
上,且∠CAB =30°,D为AB边上的动点(点D与点B不重合),连接CD,过点D作DE⊥CD交直线AC于点E.
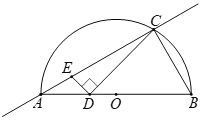
小明根据学习函数的经验,对线段AE,AD长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点D在AB上的不同位置,画图、测量,得到线段AE,AD长度的几组值,如下表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | ||
AE/cm | 0.00 | 0.41 | 0.77 | 1.00 | 1.15 | 1.00 | 0.00 | 1.00 | 4.04 | … |
AD/cm | 0.00 | 0.50 | 1.00 | 1.41 | 2.00 | 2.45 | td style="width:10%; border-top-style:solid; border-top-width:0.75pt; border-right-style:solid; border-right-width:0.75pt; border-left-style:solid; border-left-width:0.75pt; padding:3.38pt 5.03pt; vertical-align:middle">3.21 | 3.50 | … |
在AE,AD的长度这两个量中,确定_______的长度是自变量,________的长度是这个自变量的函数;
(2)在下面的平面直角坐标系![]() 中,画出(1)中所确定的函数的图象;
中,画出(1)中所确定的函数的图象;
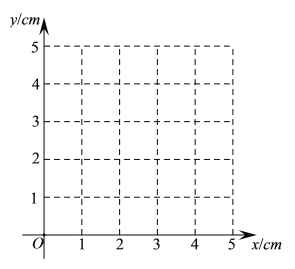
(3)结合画出的函数图象,解决问题:当AE=![]() AD时,AD的长度约为________cm(结果精确到0.1).
AD时,AD的长度约为________cm(结果精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和实数
和实数![]() ,给出如下定义:当
,给出如下定义:当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆,称为点
为半径的圆,称为点![]() 的
的![]() 倍相关圆.
倍相关圆.
例如,在如图1中,点![]() 的1倍相关圆为以点
的1倍相关圆为以点![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
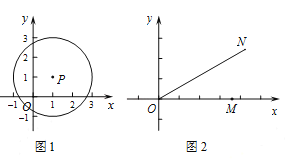
(1)在点![]() 中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
(2)如图2,若![]() 是
是![]() 轴正半轴上的动点,点
轴正半轴上的动点,点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,判断直线
,判断直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系,并证明.
倍相关圆的位置关系,并证明.
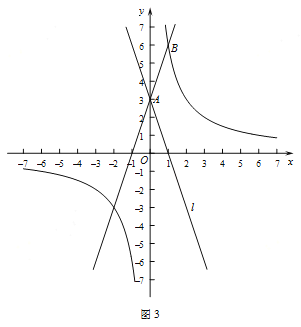
(3)如图3,已知点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的3倍相关圆的半径为________.
的3倍相关圆的半径为________.
②点![]() 在直线
在直线![]() 上,点
上,点![]() 的
的![]() 倍相关圆的半径为
倍相关圆的半径为![]() ,若点
,若点![]() 在运动过程中,以点
在运动过程中,以点![]() 为圆心,
为圆心,![]() 为半径的圆与反比例函数
为半径的圆与反比例函数![]() 的图象最多有两个公共点,直接写出
的图象最多有两个公共点,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
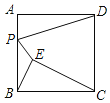
【题目】如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
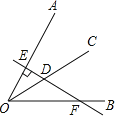
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=10,P为射线AB上一点,连接PD、AC,且PD、AC交于点E,过点A作AF⊥PD,垂足为点F.
(1)当点F落在BC边上时,求AP的值
(2)当△PAE为等腰三角形时,求AP的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com