
 如图,O是矩形ABCD对角线的交点,∠AOB=60°,AE平分∠BAD,求∠AEO的度数.
如图,O是矩形ABCD对角线的交点,∠AOB=60°,AE平分∠BAD,求∠AEO的度数. 分析 根据矩形的性质可得:OB=OC,AD∥BC,∠ABC=∠BAD=90°,又由AE平分∠BAD,∠AOB=60°,求出∠OBE与∠AEB的度数,证出△OAB是等边三角形,△ABE是等腰三角形,得出△OBE是等腰三角形,求得∠OEB的度数,则问题得解.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=∠BAD=90°,AC=BD,OB=$\frac{1}{2}$BD,OC=$\frac{1}{2}$AC,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°.
点评 此题考查了矩形的性质、等腰三角形的性质、等边三角形的判定与性质.熟练掌握矩形的性质,由等腰三角形的性质求出∠OEB是解决问题的关键.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
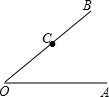 我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.
我市规划局要新建两条马路,如图所示,准备过游乐场C修一条与OA平行的马路,这条马路与∠AOB的平分线有一交点D,计划再OA边上建一个购物商场E,且使D到E最近,请利用量角器和三角板画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com