
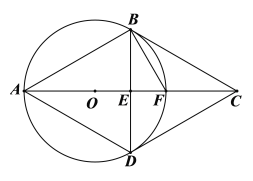
【题目】如图,菱形ABCD对角线交于点E,△ABD的外接圆⊙O交AC于点F.若FB=FC.
(1)证明:![]() =FEFA;
=FEFA;
(2)证明:BC是⊙O的切线;
(3)若EF=2,求出四边形ABCD的面积.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)首先根据菱形的性质和圆周角定理的推论得出△BEF∽△ABF,则有![]() ,即
,即![]() ,又因为FB=FC,则结论可证;
,又因为FB=FC,则结论可证;
(2)首先根据等腰三角形的性质和等量代换得出∠ABO=∠FBC,又因为∠ABO+∠FBO=∠ABF=90°,则有∠CBF+∠FBO =90°,进而可证明结论;
(3)首先根据三角形外角的性质和三角形内角和定理得出∠BAF=30°,∠BFA =60°,然后解直角三角形可求出AE,BE的长度,进而可求AC,BD的长度,最后利用菱形的面积公式即可求解.
(1)证明:∵四边形ABCD是菱形,
∴AC垂直平分BD,
∵AF为⊙O的直径.
∴∠ABF=90°.
![]() ,
,
∴△BEF∽△ABF.
∴![]() .
.
∴![]() .
.
∵FB=FC,
∴![]() =FEFA;
=FEFA;
(2)证明:连接OB,

∵OB=OA,FB=FC,BA=BC,
∴∠OBA=∠BAC,∠FBC=∠FCB,∠BAC=∠BCA.
∴∠ABO=∠FBC.
∵∠ABO+∠FBO=∠ABF=90°.
∴∠CBF+∠FBO =90°.
∴OB⊥BC.
∴BC是⊙O的切线;
(3)解:由(2)得∠BAC=∠BCA=∠FBC.
∴∠BFA=∠FBC+∠FCB=2∠FCB=2∠BAC.
∵∠BAF+∠BFA=180°-∠ABF=90°.
∴3∠BAF=90°.
∴∠BAF=30°.
∴∠BFA=2∠BAF=60°.
在Rt△BFE中,BE=EF![]() tan∠BFE=2
tan∠BFE=2![]() =
=![]() .
.
在Rt△BAE中,AE=![]() .
.
∴AC=2AE=12,BD=2BE=![]() .
.
∴四边形ABCD的面积S=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).

查看答案和解析>>
科目:初中数学 来源: 题型:
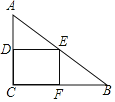
【题目】如图,在RT△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E为AB的中点,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
A.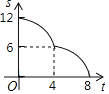 B.
B.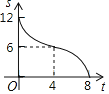
C.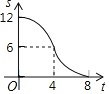 D.
D.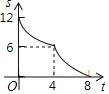
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划厂家购买A、B两种型号的电脑,已知每台A种型号电脑比每台B种型号电脑多01.万元,且用10万元购买A种型号电脑的数量与用8万元购买B种型号电脑的数量相同;
(1)求A、B两种型号电脑单价各为多少万元?
(2)学校预计用不多于9.2万元的资金购进20台电脑,其中A种型号电脑至少要购进10台,请问有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
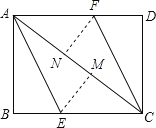
【题目】如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF折叠,使点D落在AC上的点N处.
(1)求证:四边形AECF是平行四边形;
(2)当AB与AC满足怎样数量关系时,四边形AECF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
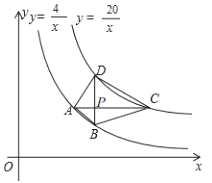
【题目】如图,四边形ABCD的四个顶点分别在反比例函数![]() 与
与![]() 的图象上,对角线
的图象上,对角线![]() 轴,且
轴,且![]() 于点P.已知点B的横坐标为4.
于点P.已知点B的横坐标为4.
(1)若点P的纵坐标为2,求直线AB的函数表达式.
(2)若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com