
| A. | ①③④ | B. | ①② | C. | ①②③ | D. | ①②④ |
分析 ①根据抛物线与x轴的交点与一元二次方程的根的关系解答即可;
②代入计算即可;
③根据开口方向和二次函数的性质解答即可;
④求出对称轴,确定x1,x2的符号.
解答 解:①∵二次函数y=2mx2+(4m-1)x-1与x轴交点的横坐标为x1,x2,∴方程2mx2+(4m-1)x-1=0有两个不相等的实数根x1,x2,①正确;
②当x=-2时,y=1,②正确;
③m的值不确定,抛物线开口方向不确定,∴当x<x1时,y的符号不确定,②不正确;
④对称轴是直线x=-$\frac{4m-1}{4m}$=-1-$\frac{1}{4m}$,随m的变化而变化,所以x1和x2的大小不确定,④不正确.
故选:B.
点评 本题考查的是二次函数的图象和性质,灵活运用性质进行解答是解题的关键,要掌握二次函数与一元二次方程的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 种类 | 单价 | 成活率 |
| 甲 | 60 | 88% |
| 乙 | 80 | 96% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
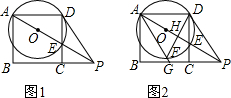 如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y.
如图1,已知ABCD是边长为4的正方形,E是CD边上的一个动点,连接AE,AE的延长线交BC的延长线于点P,连接PD.作△ADE的外接圆⊙O.设DE=x,PC=y. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com