
【题目】东坡商贸公司购进某种水果成本为20元/![]() ,经过市场调研发现,这种水果在未来48天的销售单价
,经过市场调研发现,这种水果在未来48天的销售单价![]() (元/
(元/![]() )与时间
)与时间![]() (天)之间的函数关系式
(天)之间的函数关系式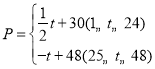 ,
,![]() 为整数,且其日销售量
为整数,且其日销售量![]() (
(![]() )与时间
)与时间![]() (天)的关系如下表:
(天)的关系如下表:
时间 | 1 | 3 | 6 | 10 | 20 | … |
日销售量 | 118 | 114 | 108 | 100 | 80 | … |
(1)已知![]() 与
与![]() 之间的变化符合一次函数关系,试求在第30天的日销售量;
之间的变化符合一次函数关系,试求在第30天的日销售量;
(2)哪一天的销售利润最大?最大日销售利润为多少?
【答案】(1)第30天的日销售量为![]() ;(2)当
;(2)当![]() 时,
时,![]()
【解析】
(1)设y=kt+b,利用待定系数法即可解决问题.
(2)日利润=日销售量×每kg利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
![]()
解得,![]() ,
,
∴y=-2t+120.
将t=30代入上式,得:y=-2×30+120=60.
所以在第30天的日销售量是60kg.
(2)设第![]() 天的销售利润为
天的销售利润为![]() 元,则
元,则![]()
当![]() 时,由题意得,
时,由题意得,![]()
=![]()
=![]()
∴t=20时,w最大值为1600元.
当![]() 时,
时,![]()
∵对称轴t=44,a=2>0,
∴在对称轴左侧w随t增大而减小,
∴t=25时,w最大值为210元,
综上所述第20天利润最大,最大利润为1600元.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(3,6)在其图象上,则(﹣3,6)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织首届“数学文化节”活动,旨在引导同学们感受数学魅力,提升数学素养,活动中,九年级全体同学参加了“趣味数学知识竞赛”.活动中获得“数学之星”称号的小颖得到了![]() 四枚纪念章,(除头像外完全相同),如图所示,四枚纪念章上分别印有四位数学家的头像,她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹,求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率.(提示:答题时可用序号
四枚纪念章,(除头像外完全相同),如图所示,四枚纪念章上分别印有四位数学家的头像,她将纪念章背面朝上放在桌面上,然后从中随机选取两枚送给妹妹,求小颖送给妹妹的两枚纪念章中恰好有一枚印有华罗庚头像的概率.(提示:答题时可用序号![]() 表示相应的纪念章)
表示相应的纪念章)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
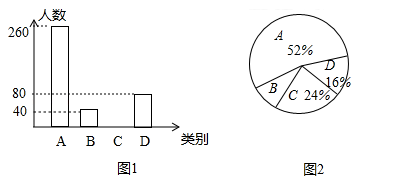
请根据图中信息回答下面的问题:
(1)本次抽样调查了多少户贫困户?
(2)抽查了多少户C类贫困户?并补全统计图;
(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?
(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】萧山区垃圾分类掀起“绿色革命”为调查居民对垃圾分类的了解情况,调查小组对某小区进行抽样调查并将调查结果绘制成了统计图(如图).已知调查中“基本了解”的人数占调查人数的60%.
(1)计算此次调查人数,并补全统计图;
(2)若该小区有住户1000人,请估计该小区对垃圾分类“基本了解”的人数.
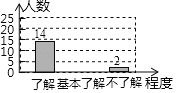
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O(0,0),点A(﹣3,0).已知抛物线y=﹣x2+2mx+3(m为常数),顶点为P.
(1)当抛物线经过点A时,顶点P的坐标为 ;
(2)在(1)的条件下,此抛物线与x轴的另一个交点为点B,与y轴交于点C.点Q为直线AC上方抛物线上一动点.
①如图1,连接QA、QC,求△QAC的面积最大值;
②如图2,若∠CBQ=45°,请求出此时点Q坐标.
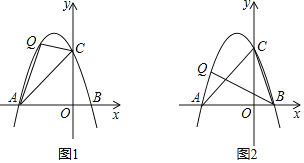
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com