
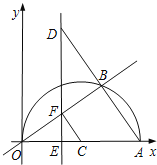
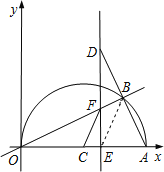
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��20��0������OAΪֱ���ڵ�һ����������ԲC����B�Ǹð�Բ����һ���㣬����OB��AB�����ӳ�AB����D��ʹDB=AB������D��x�ᴹ�ߣ��ֱ�x�ᡢֱ��OB�ڵ�E��F����EΪ���㣬����CF��
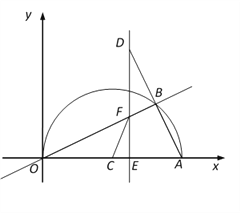
��1������AOB=30��ʱ����OB�ij��ȣ�
��2����DE=16ʱ�����߶�EF�ij���
��3���ڵ�B�˶������У��Ƿ�����Ե�E��C��FΪ��������������AOB���ƣ������ڣ��������
ʱ��E�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]() ;��2��6��24;��3��E��Ϊ
;��2��6��24;��3��E��Ϊ![]()
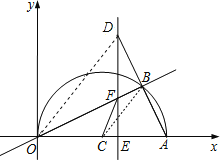
���������������: ��1������BC������֪�á�ACB=2��AOB=60�㣬AC=![]() AO=10�����ݻ�����ʽ��⣻
AO=10�����ݻ�����ʽ��⣻
��2������OD���ɴ�ֱƽ���ߵ����ʵ�OD=OA=20����DE=16����Rt��ODE�У��ɹ��ɶ�����OE��������֤����OEF�ס�DEA���������Ʊ���EF��
��3�����ڣ����Ե�E��C��FΪ��������������AOB����ʱ����Ϊ�ٵ�����E��O��C֮��ʱ�����Ե�E��C��FΪ��������������AOB���ƣ��С�ECF=��BOA���ECF=��OAB���ڵ�����E�ڵ�C���Ҳ�ʱ��Ҫʹ��ECF���BAO���ƣ�ֻ��ʹ��ECF=��BAO���۵�����E�ڵ�O�����ʱ��Ҫʹ��ECF���BAO���ƣ�ֻ��ʹ��ECF=��BAO������������ֱ���E�����꣮
�������: (1)����BC,
��A(20,0)����OA=20��CA=10��
�ߡ�AOB=30�㣬
���ACB=2��AOB=60�㣬
�AB�ij�=![]() =
=![]() ��
��
(2)����D�ڵ�һ���ޣ�
����OD��
��OA�ǡ�Cֱ��,
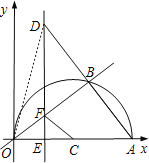
���OBA=90�㣬
�֡�AB=BD��
��OB��AD�Ĵ�ֱƽ���ߣ�
��OD=OA=20��
��Rt��ODE��
OE=![]() =
=![]() ��
��
��AE=AOOE=2012=8��
�ɡ�AOB=��ADE=90����OAB����OEF=��DEA��
�á�OEF�ס�DEA��
��![]() ,��
,��![]() ��
��
��EF=6��
����D�ڵڶ����ޣ�
����OD,
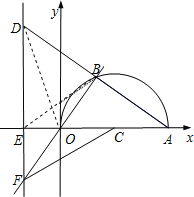
��OA�ǡ�Cֱ����
���OBA=90�㣬
�֡�AB=BD��
��OB��AD�Ĵ�ֱƽ���ߣ�
��OD=OA=10��
��Rt��ODE��
OE=![]() =
=![]() ��
��
��AE=AO+OE=20+12=32��
�ɡ�AOB=��ADE=90����OAB����OEF=��DEA��
�á�OEF�ס�DEA
��![]() ,��
,��![]() ��
��
��EF=24��
��EF=6��24��
(3)��OE=x��
�ٵ�����E��O��C֮��ʱ�����Ե�E. C.FΪ���������
�����AOB���ƣ��С�ECF=��BOA���ECF=��OAB��
����ECF=��BOAʱ����ʱ��OCFΪ���������Σ���EΪOC
�е�,��OE=5��
��E (5,0)��
����ECF=��OABʱ����CE=10x��AE=20x��
��CF��AB,��CF=![]() AB��
AB��
�ߡ�ECF�ס�EAD��
��![]() ,��
,��![]() ,��ã�x=
,��ã�x=![]() ��
��
��E (![]() ,0)��
,0)��
�ڵ�����E�ڵ�C���Ҳ�ʱ��
�ߡ�ECF>��BOA��
��Ҫʹ��ECF���BAO����,ֻ��ʹ��ECF=��BAO,
����BE��
��BEΪRt��ADEб���ϵ����ߣ�
��BE=AB=BD��
���BEA=��BAO��
���BEA=��ECF��
��CF��BE��
��![]() ��
��
�ߡ�ECF=��BAO,��FEC=��DEA=90�㣬
���CEF�ס�AED��
��CFAD=CEAE��
��AD=2BE��
��![]() ��
��
��![]() ,���x =
,���x =![]() ,x =
,x =![]() <0(��ȥ)��
<0(��ȥ)��
��E (![]() ,0)��
,0)��
�۵�����E�ڵ�O�����ʱ��
�ߡ�BOA=��EOF>��ECF.
��Ҫʹ��ECF���BAO����,ֻ��ʹ��ECF=��BAO

����BE,��BE=![]() AD=AB����BEA=��BAO
AD=AB����BEA=��BAO
���ECF=��BEA��
��CF��BE��
��![]() ��
��
�֡ߡ�ECF=��BAO,��FEC=��DEA=90��
���CEF�ס�AED��
��![]() ��
��
��AD=2BE��
��![]() ��
��
��![]() ��
��
���x=![]() ,x=
,x=![]() (��ȥ)��
(��ȥ)��
�ߵ�E��x�Ḻ�����ϣ�
��![]() (
(![]() ,0)��
,0)��
���������������Ե�E. C.FΪ��������������AOB���ƣ�
��ʱ��E����Ϊ��E��Ϊ![]() .
.
�㾦: �����Ĺؼ��������������������ε����ʣ����������εĶ�Ӧ�߳ɱ�����ע���Ӧ��ĸ�ڶ�Ӧλ����.


 ������ϵ�д�
������ϵ�д� �±�Сѧ��Ԫ�Բ���ϵ�д�
�±�Сѧ��Ԫ�Բ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=mx+4��ͼ����x���ཻ�ڵ�A���뷴��������y=![]()
![]() ��ͼ���ཻ�ڵ�B��1��6����
��ͼ���ཻ�ڵ�B��1��6����
��1����һ�κ����ͷ����������Ľ���ʽ��
��2�����P��x����һ�㣬��S��APB=18��ֱ��д����P�����꣮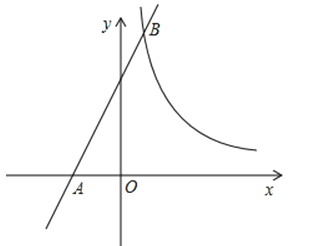
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͬһ��������![]() ��
��![]() ��
��![]() �������������Ҫ����ֱ�ߺ�Բ����ͼ��
�������������Ҫ����ֱ�ߺ�Բ����ͼ��
�ٻ��߶�![]() ��
�� ![]() ��
��
��������![]() ����������
����������![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ��
��
��������![]() ����������
����������![]() ��ȡһ��
��ȡһ��![]() ��ʹ
��ʹ![]() ��
��
�����������ͼ������������⣺
��![]() ������
������![]() ��
��![]() �ֱ����������߶ε��е㣿��˵���ɣ�
�ֱ����������߶ε��е㣿��˵���ɣ�
��![]() ������֪�߶�
������֪�߶�![]() �ij�Ϊ
�ij�Ϊ![]() �����߶�
�����߶�![]() �ij��ȣ�
�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��mΪ��������ͼ����һ�������ޣ�
��mΪ��������ͼ����һ�������ޣ�
��1����m��ȡֵ��Χ��
��2����ͼ�����÷�����������ͼ��ABOD�Ķ���D����A��B������ֱ�Ϊ��0��4��������3��0����
�������������ʽ��
�����P�Ǹ÷���������ͼ���ϵ�һ�㣬��OD=OP����P�������Ϊ���٣�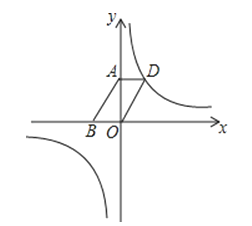
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѷ���ʽ5x2y3��2x4y2+7+3x5y��x�Ľ������к������ǣ�������
A.5x2y3
B.��2x4y2
C.7
D.3x5y
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣�Ϊ�ٰ�У�Ļ����������ס������������ϳ�ͬѧ�����ݳ���װ��һ��һ�ף������92�ˣ����мװ���Ұ��˶����Ҽװ��90�ˣ��������ǹ����̸������ݳ���װ�ļ۸����

����������ÿλͬѧ����һ��װ����ôһ��Ӧ��5020Ԫ��
��1���ס�����������������ÿλͬѧ����һ��װ���ȵ���������Խ�ʡ����Ǯ��
��2���ס���������ж�����ͬѧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ![]() �У�
�� ![]() ����
����![]() Ϊֱ����
Ϊֱ����![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() �����߽�
�����߽�![]() ��
��![]() ��
��
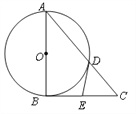
��1����֤�� ![]() ����2����
����2����![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ����ȷ���ǣ� ��
A.��a��b��2=a2��2ab+b2
B.��a��b��2=a2��b2
C.��a��b��2=a2+2ab+b2
D.��a��b��2=a2��ab+b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ѷ���ʽx3��xy2+x2y+x4��3��x�Ľ������У���ȷ���ǣ�������
A.x4+x3+x2y��3��xy2
B.��xy2+x2y+x4+x3��3
C.��3��xy2+x2y+x3+x4
D.x4+x3+x2y��xy2��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com