
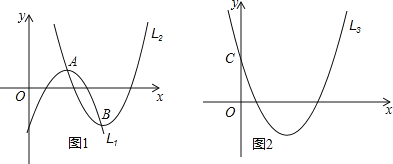
°æƒø°ø»ÁÕº1£¨»Ù≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£®µ„A”ε„B≤ª÷ÿ∫œ£©Œ“√«∞—’‚—˘µƒ¡Ω≈◊ŒÔœþL1°¢L2ª•≥∆Œ™°∞”—∫√°±≈◊ŒÔœþ£¨ø…º˚“ªÃı≈◊ŒÔœþµƒ°∞”—∫√°±≈◊ŒÔœþø…“‘”–∫Ð∂ýÃı£Æ
£®1£©»ÁÕº2£¨“—÷™≈◊ŒÔœþL3£∫y=2x2-8x+4”Îy÷·Ωª”⁄µ„C£¨ ‘«Û≥ˆµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±Í£ª
£®2£©«Î«Û≥ˆ“‘µ„DŒ™∂•µ„µƒL3µƒ°∞”—∫√°±≈◊ŒÔœþL4µƒΩ‚Œˆ Ω£¨≤¢÷∏≥ˆL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
£®3£©»Ù≈◊ŒÔy=a1£®x-m£©2+nµƒ»Œ“‚“ªÃı°∞”—∫√°±≈◊ŒÔœþµƒΩ‚Œˆ ΩŒ™y=a2£®x-h£©2+k£¨«Î–¥≥ˆa1”Îa2µƒπÿœµ Ω£¨≤¢Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©£®4£¨4£©£ª£®2£©2°Ðx°Ð4£ª£®3£©a1=-a2£¨¿Ì”…»Áœ¬£∫º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©…Ëx£Ω0£¨«Û≥ˆyµƒ÷µ£¨º¥ø…µ√µΩCµƒ◊¯±Í£¨∞—≈◊ŒÔœþL3£∫y£Ω2x28x£´4≈‰∑Ωº¥ø…µ√µΩ≈◊ŒÔœþµƒ∂‘≥∆÷·£¨”…¥Àø…«Û≥ˆµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±Í£ª
£®2£©”…£®1£©ø…÷™µ„Dµƒ◊¯±ÍŒ™£®4£¨4£©£¨‘Ÿ”…Ãıº˛“‘µ„DŒ™∂•µ„µƒL3µƒ°∞”—∫√°±≈◊ŒÔœþL4µƒΩ‚Œˆ Ω£¨ø…«Û≥ˆL4µƒΩ‚Œˆ Ω£¨Ω¯∂¯ø…«Û≥ˆL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß£ª
£®3£©∏˘æð£∫≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£¨ø…“‘¡–≥ˆ¡Ω∏ˆ∑Ω≥㨜ýº”ø…µ√£∫£®a1£´a2£©£®mh£©2£Ω0£¨ø…µ√a1£Ωa2.
Ω‚£∫£®1£©°þ≈◊ŒÔœþL3£∫y=2x2-8x+4£¨
°ýy=2£®x-2£©2-4£¨
°ý∂•µ„Œ™£®2£¨4£©£¨∂‘≥∆÷·Œ™x=2£¨
…Ëx=0£¨‘Úy=4£¨
°ýC£®0£¨4£©£¨
°ýµ„Cπÿ”⁄∏√≈◊ŒÔœþ∂‘≥∆÷·∂‘≥∆µƒ∂‘≥∆µ„Dµƒ◊¯±ÍŒ™£∫£®4£¨4£©£ª
£®2£©°þ“‘µ„D£®4£¨4£©Œ™∂•µ„µƒ≈◊ŒÔœþL4π˝µ„£®2£¨-4£©£¨
…ËL4µƒΩ‚Œˆ Ω![]() £¨
£¨
Ω´µ„£®2£¨-4£©¥˙»ÎL4ø…µ√£¨a=-2£¨
°ýL4µƒΩ‚Œˆ ΩŒ™y=-2£®x-4£©2+4£¨
L3”ÎL4µƒ¡Ω∏ˆΩªµ„∑÷±Œ™£®4£¨4£©∫Õ£®2£¨-4£©
°ýL3”ÎL4÷–yÕ¨ ±ÀÊx‘ˆ¥Û∂¯‘ˆ¥Ûµƒ◊‘±‰¡øµƒ»°÷µ∑∂Œß «£∫2°Ðx°Ð4 ±£ª
£®3£©a1=-a2£¨
¿Ì”…»Áœ¬£∫
°þ≈◊ŒÔœþL1µƒ∂•µ„A‘⁄≈◊ŒÔœþL2…œ£¨≈◊ŒÔœþL2µƒ∂•µ„B“≤‘⁄≈◊ŒÔœþL1…œ£¨
°ýø…“‘¡–≥ˆ¡Ω∏ˆ∑Ω≥Ã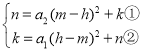 £¨
£¨
¢Ÿ+¢⁄µ√£∫£®a1+a2£©£®m-h£©2=0£¨
°ýa1=-a2£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨÷±œþ![]() ”Î
”Î![]() ÷·£¨
÷·£¨![]() ÷·∑÷±œýΩª”⁄
÷·∑÷±œýΩª”⁄![]() £¨
£¨![]() ¡Ωµ„£¨”Î∑¥±»¿˝∫Ø ˝
¡Ωµ„£¨”Î∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛΩª”⁄µ„
µƒÕºœÛΩª”⁄µ„![]() £¨µ„
£¨µ„![]() µƒ∫·◊¯±ÍŒ™4£Æ
µƒ∫·◊¯±ÍŒ™4£Æ
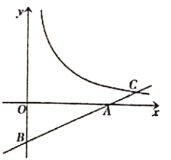
£®1£©«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©π˝µ„![]() ◊˜
◊˜![]() ÷·£¨¥π◊„Œ™
÷·£¨¥π◊„Œ™![]() £¨µ„
£¨µ„![]() «∏√∑¥±»¿˝∫Ø ˝
«∏√∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛ…œ“ªµ„£¨¡¨Ω”
µƒÕºœÛ…œ“ªµ„£¨¡¨Ω”![]() £¨
£¨![]() £¨«“
£¨«“![]() £Æ
£Æ
¢Ÿ«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
¢⁄«Ûµ„![]() µΩ÷±œþ
µΩ÷±œþ![]() µƒæý¿Î
µƒæý¿Î![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄µ»—¸Ãð–Œ![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £¨
£¨![]() ∑÷±Œ™…œ°¢œ¬¡Ωµ◊
∑÷±Œ™…œ°¢œ¬¡Ωµ◊![]() £¨
£¨![]() µƒ÷–µ„£¨
µƒ÷–µ„£¨![]() £¨
£¨![]() ∑÷±Œ™
∑÷±Œ™![]() £¨
£¨![]() µƒ÷–µ„£¨«Û÷§£∫Àƒ±þ–Œ
µƒ÷–µ„£¨«Û÷§£∫Àƒ±þ–Œ![]() «¡‚–Œ£Æ
«¡‚–Œ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
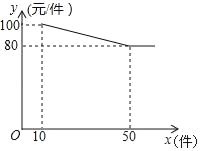
°æƒø°ø∑˛◊∞≥ß≈˙∑¢ƒ≥÷÷∑˛◊∞£¨√øº˛≥…±æŒ™65‘™£¨πÊ∂®≤ªµÕ”⁄10º˛ø…“‘≈˙∑¢£¨∆‰≈˙∑¢º€y£®‘™/º˛£©”Î≈˙∑¢ ˝¡øx£®º˛£©£®xŒ™’˝’˚ ˝£©÷ƺ‰À˘¬˙◊„µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ æ£Æ
£®1£©«Ûy”Îx÷ƺ‰À˘¬˙◊„µƒ∫Ø ˝πÿœµ Ω£¨≤¢–¥≥ˆxµƒ»°÷µ∑∂Œß£ª
£®2£©…Ë∑˛◊∞≥ßÀ˘ªÒ¿˚»ÛŒ™w£®‘™£©£¨»Ù10°Ðx°Ð50£®xŒ™’˝’˚ ˝£©£¨«Û≈˙∑¢∏√÷÷∑˛◊∞∂ý…Ÿº˛ ±£¨∑˛◊∞≥ߪҵ√¿˚»Û◊Ó¥Û£ø◊Ó¥Û¿˚»Û «∂ý…Ÿ‘™£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ‚œ¬¡–∑Ω≥ã®◊È£©£∫
£®1£©£®x+3£©£®x+1£©£Ω1£ª
£®2£©![]() ©Å1£Ω
©Å1£Ω![]() £ª
£ª
£®3£©![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™![]() £¨“‘
£¨“‘![]() Œ™÷±æ∂µƒ
Œ™÷±æ∂µƒ![]() Ωª±þ
Ωª±þ![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() ”Î
”Î![]() œý«–£Æ
œý«–£Æ
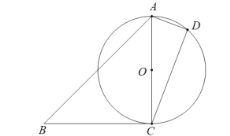
£®1£©»Ù![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
£®2£©µ„![]() «
«![]() …œ“ªµ„£¨µ„
…œ“ªµ„£¨µ„![]() ¡Ωµ„‘⁄
¡Ωµ„‘⁄![]() µƒ“Ï≤ý£Æ»Ù
µƒ“Ï≤ý£Æ»Ù![]() £¨
£¨![]() £¨
£¨![]() £¨«Û
£¨«Û![]() ∞Îæ∂µƒ≥§£Æ
∞Îæ∂µƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
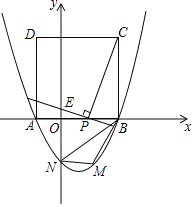
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝![]() µƒÕºœÛ”Î
µƒÕºœÛ”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() ∫Õµ„
∫Õµ„![]() £¨”Î
£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨“‘
£¨“‘![]() Œ™±þ‘⁄
Œ™±þ‘⁄![]() ÷·…œ∑Ω◊˜’˝∑Ω–Œ
÷·…œ∑Ω◊˜’˝∑Ω–Œ![]() £¨µ„
£¨µ„![]() «
«![]() ÷·…œ“ª∂ص„£¨¡¨Ω”
÷·…œ“ª∂ص„£¨¡¨Ω”![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() µƒ¥πœþ”Î
µƒ¥πœþ”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £Æ
£Æ
£®1£©«Û∏√≈◊ŒÔœþµƒ∫Ø ˝πÿœµ±Ì¥Ô Ω£ª
£®2£©µ±µ„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() £®µ„
£®µ„![]() ≤ª”Î
≤ª”Î![]() ÷ÿ∫œ£©…œ‘À∂Ø÷¡∫Œ¥¶ ±£¨œþ∂Œ
÷ÿ∫œ£©…œ‘À∂Ø÷¡∫Œ¥¶ ±£¨œþ∂Œ![]() µƒ≥§”–◊Ó¥Û÷µ£ø≤¢«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£ª
µƒ≥§”–◊Ó¥Û÷µ£ø≤¢«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£ª
£®3£©‘⁄µ⁄ÀƒœÛœÞµƒ≈◊ŒÔœþ…œ»Œ»°“ªµ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £Æ«ÎŒ £∫
£Æ«ÎŒ £∫![]() µƒ√ʪ˝ «∑ҥʑ⁄◊Ó¥Û÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ¥À ±µ„
µƒ√ʪ˝ «∑ҥʑ⁄◊Ó¥Û÷µ£ø»Ù¥Ê‘⁄£¨«Û≥ˆ¥À ±µ„![]() µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
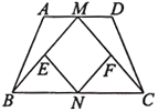
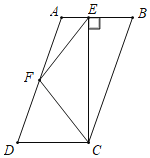
°æƒø°ø»ÁÕº£¨‘⁄ABCD÷–£¨AD£Ω2AB£¨F «ADµƒ÷–µ„£¨◊˜CE°ÕAB£¨¥π◊„E‘⁄œþ∂ŒAB…œ£¨¡¨Ω”EF°¢CF£¨‘Úœ¬¡–Ω·¬€÷–“ª∂®≥…¡¢µƒ «_____£®∞—À˘”–’˝»∑Ω·¬€µƒ–Ú∫≈≤øÃÓ‘⁄∫·œþ…œ£©£Æ¢Ÿ°œAEF£Ω![]() °œDFE£ª¢⁄S°˜BEC£Ω2S°˜CEF£ª¢€EF£ΩCF£ª¢Ð°œBCD£Ω2°œDCF£Æ
°œDFE£ª¢⁄S°˜BEC£Ω2S°˜CEF£ª¢€EF£ΩCF£ª¢Ð°œBCD£Ω2°œDCF£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ˙º“◊‘2016ƒÍ1‘¬1»’∆ µ––»´√Ê∑≈ø™∂˛Ã•’˛≤þ£¨ƒ≥º∆…˙◊È÷ØŒ™¡ÀΩ‚∏√ –º“Õ•∂‘¥˝’‚œÓ’˛≤þµƒÃ¨∂»£¨◊º±∏≤…”√“‘œ¬µ˜≤È∑Ω Ω÷–µƒ“ª÷÷Ω¯––µ˜≤È£∫
A£Æ¥”“ª∏ˆ…Á«¯Àʪ˙—°»°1 000ªßº“Õ•µ˜≤È£ª
B£Æ¥”“ª∏ˆ≥«’Úµƒ≤ªÕ¨◊°’¨¬•÷–Àʪ˙—°»°1 000ªßº“Õ•µ˜≤È£ª
C£Æ¥”∏√ –π´∞≤æ÷ªßºÆπп̥¶Àʪ˙≥È»°1 000ªß≥«œÁº“Õ•µ˜≤È£Æ
£®1£©‘⁄…œ ˆµ˜≤È∑Ω Ω÷–£¨ƒ„»œŒ™±»Ωœ∫œ¿Ìµƒ“ª∏ˆ «°æ1°ø£Æ£®ÃÓ°∞A°±°¢°∞B°±ªÚ°∞C°±£©
£®2£©Ω´“ª÷÷±»Ωœ∫œ¿Ìµƒµ˜≤È∑Ω Ωµ˜≤ȵ√µΩµƒΩ·π˚∑÷Œ™Àƒ¿ý£∫£®A£©“—”–¡Ω∏ˆ∫¢◊”£ª
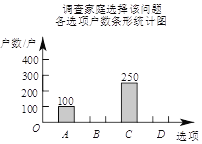
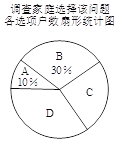
£®B£©æˆ∂®…˙∂˛Ã•£ª£®C£©øº¬«÷Æ÷–£ª£®D£©æˆ∂®≤ª…˙∂˛Ã•£ÆΩ´µ˜≤ÈΩ·π˚ªÊ÷∆≥…»Áœ¬¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ
«Î∏˘æð“‘…œ≤ªÕÍ’˚µƒÕ≥º∆ÕºÃ·π©µƒ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
¢Ÿ≤π»´Ãı–ŒÕ≥º∆Õº£Æ
¢⁄π¿º∆∏√ –100Õڪߺ“Õ•÷–æˆ∂®≤ª…˙∂˛Ã•µƒº“Õ• ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com