
分析 先由$\overline{x}$=$\frac{1}{n}$(x1+x2+x3+…xn),得出x1+x2+x3+…xn=n$\overline{x}$,再根据平均数的定义即可求解.
解答 解:∵$\overline{x}$=$\frac{1}{n}$(x1+x2+x3+…xn),
∴x1+x2+x3+…xn=n$\overline{x}$,
∴ax1+b,ax2+b,ax3+b,…,axn+b的平均数为:
$\frac{1}{n}$(ax1+b+ax2+b+ax3+b+…+axn+b)=$\frac{1}{n}$[a(x1+x2+x3+…xn)+nb]=$\frac{1}{n}$[a•n$\overline{x}$+nb]=a$\overline{x}$+b,
故答案为a$\overline{x}$+b.
点评 本题考查了平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.
如图,在△ABC中,若DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,且S△ADE=4cm2,则四边形BCED的面积为32cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.
如图,已知?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE;②∠A=∠BHE;③AB=BH;④BH=HG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
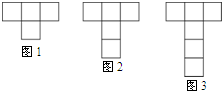 如图是经典手机游戏“俄罗斯方块”中的图案,图1中有8个矩形,图2中有11个矩形,图3中有15个矩形,根据此规律,图5中共有( )个矩形.
如图是经典手机游戏“俄罗斯方块”中的图案,图1中有8个矩形,图2中有11个矩形,图3中有15个矩形,根据此规律,图5中共有( )个矩形.| A. | 19 | B. | 25 | C. | 26 | D. | 31 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com