
 如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.
如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.分析 (1)首先连接OD,根据等边对等角得出∠B=∠ODB,又由等腰三角形ABC的底角为30°,可得∠A=∠ODB,即可证得OD∥AC,继而可证得结论;
(2)由以BC为直径的⊙O,可得CD⊥AB,又由等腰三角形ABC的底角为30°,可得AD=BD=$\frac{1}{2}$AB=2$\sqrt{3}$,通过解余弦函数求得BC,从而得出圆的半径,进而根据S阴影=S扇形OCD-S△OCD即可求得.
解答 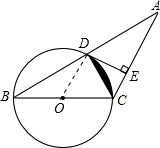 (1)证明:连接OD.
(1)证明:连接OD.
∵OB=OD,
∴∠OBD=∠ODB.又∵∠A=∠B=30°,
∴∠A=∠ODB,
∴DO∥AC,
∵DE⊥AC,
∴OD⊥DE.
∴DE 为⊙O 的切线;
(2)解:∵BC 为直径,
∴∠BDC=90°.
根据等腰三角形的三线合一性质得到CD是AB的中线,
∴BD=$\frac{1}{2}$AB=2$\sqrt{3}$,
在直角三角形BDC中,cosB═$\frac{BD}{BC}$,即$\frac{\sqrt{3}}{2}$=$\frac{2\sqrt{3}}{BC}$,
解得BC=4,
S阴影=S扇形OCD-S△OCD=$\frac{60π×{2}^{2}}{360}$-$\frac{1}{2}$×$2×\sqrt{3}$=$\frac{2π}{3}$-$\sqrt{3}$.
点评 此题考查了切线的判定、等腰三角形的性质、三角函数以及扇形的面积等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
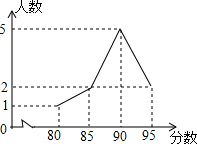 在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )
在一次演讲比赛中,参赛的10名学生成绩统计如图所示,下列说法中错误的是( )| A. | 众数是90分 | B. | 中位数是90分 | C. | 平均数是90分 | D. | 极差是15分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
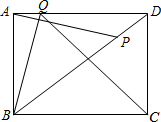 如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).
如图,矩形ABCD中,AB=6,AD=8,动点P从点D出发,以每秒5个单位的速度向点B匀速运动,同时动点Q从点A出发,以每秒4个单位的速度向点D匀速运动,运动的时间为t秒(0<t<2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
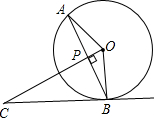 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的切线交OP的延长线于点C.
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的切线交OP的延长线于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com