
 在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.
在平面直角坐标系xOy中,抛物线y=$\frac{1}{2}{x^2}$-x+2与y轴交于点A,顶点为点B,点C与点A关于抛物线的对称轴对称.分析 (1)欲求直线BC的解析式,需要求得点B、C的坐标,由抛物线解析式求得点A、B的坐标,然后根据点的对称性得到点C的坐标;然后由待定系数法来求直线方程;
(2)根据抛物线解析式y=$\frac{1}{2}{x^2}$-x+2易求D(4,6),由直线y=$\frac{1}{2}$x+1易求点(0,1),点F(4,3).设点A平移后的对应点为点A′,点D平移后的对应点为点D′.当图象G向下平移至点A′与点E重合时,点D'在直线BC上方,此时t=1.当图象G向下平移至点D′与点F重合时,点A′在直线BC下方,此时t=3.结合图象可知,符合题意的t的取值范围是1<t≤3.
解答 解:(1)∵抛物线$y=\frac{1}{2}{x^2}-x+2$与y轴交于点A,?
∴点A的坐标为(0,2).
∵$y=\frac{1}{2}{x^2}-x+2=\frac{1}{2}{(x-1)^2}+\frac{3}{2}$,
∴抛物线的对称轴为直线x=1,顶点B的坐标为(1,$\frac{3}{2}$).
又∵点C与点A关于抛物线的对称轴对称,
∴点C的坐标为(2,2),且点C在抛物线上.
设直线BC的解析式为y=kx+b.
∵直线BC经过点B(1,$\frac{3}{2}$)和点C(2,2),
∴$\left\{\begin{array}{l}{k+b=\frac{3}{2}}\\{2k+b=2}\end{array}\right.$
解得$\left\{\begin{array}{l}k=\frac{1}{2}\\ b=1.\end{array}\right.$
∴直线BC的解析式为:y=$\frac{1}{2}$x+1;
(2)∵抛物线y=$\frac{1}{2}{x^2}$-x+2中,当x=4时,y=6,
∴点D的坐标为(4,6).
∵直线y=$\frac{1}{2}$x+1中,当x=0时,y=1.当x=4时,y=3,
∴如图,点E的坐标为(0,1),点F的坐标为(4,3).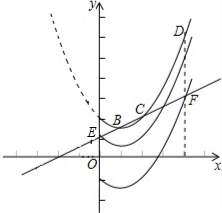
设点A平移后的对应点为点A′,点D平移后的对应点为点D′.当图象G向下平移至点A′与点E重合时,点D'在直线BC上方,
此时t=1.
当图象G向下平移至点D′与点F重合时,点A′在直线BC下方,此时t=3.
结合图象可知,符合题意的t的取值范围是1<t≤3.
点评 本题考查了待定系数法求二次函数解析式,二次函数图象的几何变换.解题时,利用了“数形结合”的数学思想,使抽象的问题变得直观化了.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
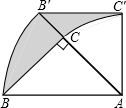 如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).
如图,在△ABC中,∠ACB=90°,BC=AC=2,以点A为旋转中心,把△ABC按顺时针方向旋转45°后得到△AB′C′,BC边在上述旋转过程中所扫过部分(阴影部分)的面积是$\frac{1}{2}$π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.
如图,已知等腰三角形ABC的底角为30,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E,连接CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com