
【题目】已知二次函数![]() (
(![]() 是常数,
是常数,![]() )的
)的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
| 0 | 2 |
| 6 | 0 |
|
| 6 |
下列结论:
①![]() ;
;
②当![]() 时,函数最小值为
时,函数最小值为![]() ;
;
③若点![]() ,点
,点![]() 在二次函数图象上,则
在二次函数图象上,则![]() ;
;
④方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)
科目:初中数学 来源: 题型:
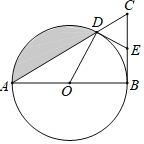
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,点E为BC的中点,连接OD、DE.
(1)求证:DE是⊙O的切线;
(2)若∠BAC=30°,AB=12,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
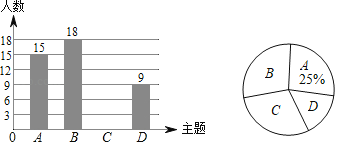
【题目】为了响应市政府号召,某校开展了“四城同创,共建美好家园”活动周,活动周设置了“A:文明礼仪,B:生态环境,C:交通安全,D:卫生保洁”四个主题,每个学生选一个主题参与.为了解活动开展情况,学校随机抽取了部分学生进行调查,并根据调查结果绘制了如下条形统计图和扇形统计图.
(1)本次随机调查的学生人数是 人;
(2)在扇形统计图中,“C”所在扇形的圆心角等于 度;
(3)如果该校共有学生2400人,请你估计参与“文明礼仪”主题的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
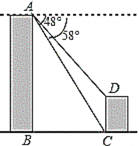
【题目】如图,甲、乙两座建筑物的水平距离![]() 为
为![]() ,从甲的顶部
,从甲的顶部![]() 处测得乙的顶部
处测得乙的顶部![]() 处的俯角为48°,测得底部
处的俯角为48°,测得底部![]() 处的俯角为53°,求甲、乙建筑物的高度
处的俯角为53°,求甲、乙建筑物的高度![]() 和
和![]() (结果用含非特珠角的三角函数表示即可).
(结果用含非特珠角的三角函数表示即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,![]() 与
与![]() 恰好为对顶角,
恰好为对顶角,![]() ,连接
,连接![]() ,
,![]() ,点F是线段
,点F是线段![]() 上一点.
上一点.
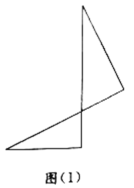
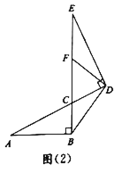
探究发现:
(1)当点F为线段![]() 的中点时,连接
的中点时,连接![]() (如图(2),小明经过探究,得到结论:
(如图(2),小明经过探究,得到结论:![]() .你认为此结论是否成立?_________.(填“是”或“否”)
.你认为此结论是否成立?_________.(填“是”或“否”)
拓展延伸:
(2)将(1)中的条件与结论互换,即:若![]() ,则点F为线段
,则点F为线段![]() 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《郑州市城市生活垃圾分类管理办法》于2019年12月起施行,某社区要投放![]() 两种垃圾桶,负责人小李调查发现:
两种垃圾桶,负责人小李调查发现:
购买数量少于 | 购买数量不少于 | |
| 原价销售 | 以原价的 |
| 原价销售 | 以原价的 |
若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需要付款
个,则共需要付款![]() 元;若购买
元;若购买![]() 种垃圾桶
种垃圾桶![]() 个,
个,![]() 种垃圾桶
种垃圾桶![]() 个,则共需付款
个,则共需付款![]() 元.
元.
(1)求![]() 两种垃圾桶的单价各为多少元?
两种垃圾桶的单价各为多少元?
(2)若需要购买![]() 两种垃圾桶共
两种垃圾桶共![]() 个,且
个,且![]() 种垃圾桶不多于
种垃圾桶不多于![]() 种垃圾桶数量的
种垃圾桶数量的![]() ,如何购买使花费最少?最少费用为多少元?请说明理由.
,如何购买使花费最少?最少费用为多少元?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
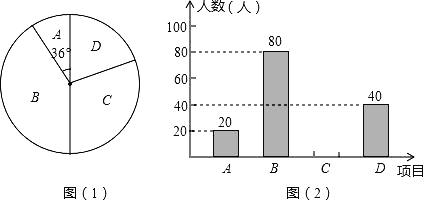
【题目】为了提高学生的综合素质,某中学成立了以下社团:A.机器人,B.围棋,C.羽毛球,D.电影配音.每人只能加入一个社团,为了解学生参加社团的情况,从参加社团的学生中随机抽取了部分学生进行调查,并将调查结果绘制成如图两幅不完整的统计图,其中图(1)中A所占扇形的圆心角为36°.
根据以上信息,解答下列问题:
(1)这次被调查的学生共有 人,B所占扇形的圆心角是 度;
(2)请你将条形统计图补充完整;
(3)若该校共有1000名学生加人了社团,请你估计这1000名学生中有多少人参加了羽毛球社团;
(4)在机器人社团活动中,由于甲、乙、丙、丁四人平时的表现优秀,现决定从这四人中任选两名参加机器人大赛,用树状图或列表法求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com