[题目]已知坐标平面内的点A(3.2).B(1.3).C(﹣1.﹣6).D(2a.4a﹣4)中只有一点不在直线l上.则这一点是( )A.点AB.点BC.点CD.点D 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】已知坐标平面内的点A（3，2），B（1，3），C（﹣1，﹣6），D（2a，4a﹣4）中只有一点不在直线l上，则这一点是（　　）

A.点AB.点BC.点CD.点D

【答案】B

【解析】

先求出直线AB和直线AC的解析式，再把点D（2a，4a-4）分别代入看是否符合即可．

解：设直线AB为y=kx+b，

把点A（3，2），B（1，3）代入得，

解得：，

即直线AB为：

由x=2a时，

可知，点D不在此函数图象上；

设直线AC为y=mx+n，

把点A（3，2），C（-1，-6）代入得，

解得，

即直线AC为：y=2x-4，

由x=2a时，y=2×2a-4=4a-4可知，点D在此函数图象上；

故A（3，2），C（-1，-6），D（2a，4a-4）在一条直线l上，点B不在直线l上，

故选：B．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某药品研究所开发一种抗菌新药，经多年动物实验，首次用于临床人体试验，测得成人服药后血液中药物浓度y（微克/毫升）与服药时间x小时之间函数关系如图所示（当4≤x≤10时，y与x成反比例）．

（1）根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式．

（2）问血液中药物浓度不低于2微克/毫升的持续时间多少小时？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在中，，的垂直平分线交于点，交于点．

（1）若，求的长；

（2）若，求证：是等腰三角形．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】设a，b是任意两个实数，规定a与b之间的一种运算“⊕”为：a⊕b=，

例如：1⊕（﹣3）==﹣3，（﹣3）⊕2=（﹣3）﹣2 =﹣5，

（x2+1）⊕（x﹣1）=（因为x2+1＞0）

参照上面材料，解答下列问题：

（1）2⊕4=　　，（﹣2）⊕4=　　；

（2）若x＞，且满足（2x﹣1）⊕（4x2﹣1）=（﹣4）⊕（1﹣4x），求x的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知AB＝AC，AE＝AF，BE与CF交于点D，则对于下列结论：①△ABE≌△ACF；②△BDF≌△CDE；③D在∠BAC的平分线上．其中正确的是（　　）

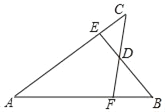
A. ① B. ② C. ①和② D. ①②③

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，直线是第一、三象限的角平分线.

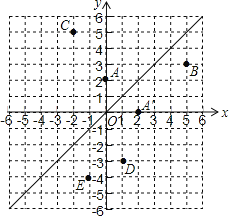
（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（-2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：___________、___________；

（2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点关于第一、三象限的角平分线的对称点的坐标为___________（不必证明）；

（3）已知两点、，试在直线L上画出点Q，使点Q到D、E两点的距离之和最小，求QD+QE的最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：

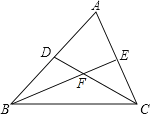
【题目】如图，在△ABC中，∠B、∠C的平分线BE，CD相交于点F．

(1)∠ABC＝40°，∠A＝60°，求∠BFD的度数；

(2)直接写出∠A与∠BFD的数量关系．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A、B重合），给出以下四个结论：①AE=CF；②△EPF是等腰直角三角形；③2S四边形AEPF=S△ABC；④BE+CF=EF．上述结论中始终正确的有（　　）