【题目】如图8，在
中， 
， 
于
， 
于D.
（1）求证：△ADC≌△CEB. （2）
，求BE的长度.
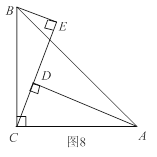
【答案】（1）证明见解析； （2）2cm.
【解析】分析：（1）根据全等三角形的判定定理AAS推知：△ADC≌△CEB；（2）利用（1）中的全等三角形的对应边相等得到：AD=CE=5cm，CD=BE．则根据图中相关线段的和差关系得到BE=AD-DE．
解析：
(1)证明：如图,∵AD⊥CE,∠ACB=90°，
∴∠ADC=∠ACB=90°，
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中，
，
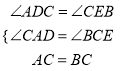∴△ADC≌△CEB(AAS)；
(2)由(1)知,△ADC≌△CEB，则AD=CE=5cm，CD=BE.
如图，∵CD=CEDE，
∴BE=ADDE=53=2(cm)，即BE的长度是2cm.
快捷英语周周练系列答案科目：初中数学 来源： 题型：
【题目】把下列各数填入相应的集合内：+8.5，-3
，0.3，0，-3.4，12，-9，4
，-1.2，-2.
（1）正数集合:｛___________…｝；
（2）整数集合:｛___________…｝；
（3）非正整数集合:｛_____________…｝；
（4）负分数集合:｛ ________________…｝.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】解方程
（1）（x-2）（x+3）=-4 （公式法） （2）2x2+4x+1=25（配方法）
（3）3（x-5）2=x-5 （4）（x+3）2=（3x-5）2．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是半圆O的直径，点P是BA延长线上一点，PC是⊙O的切线，切点为C，过点B作BD⊥PC交PC的延长线于点D，连接BC．求证：
（1）∠PBC=∠CBD；
（2）
=ABBD．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是线段AB上一点，AB=12cm，C、D两点分别从P、B出发以1cm/s、2cm/s的速度沿直线AB向左运动（C在线段AP上，D在线段BP上），运动的时间为t.
（1）当t=1时，PD=2AC，请求出AP的长；
（2）当t=2时，PD=2AC，请求出AP的长；
（3）若C、D运动到任一时刻时，总有PD=2AC，请求出AP的长；
（4）在（3）的条件下，Q是直线AB上一点，且AQ﹣BQ=PQ，求PQ的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，三角形DEF是三角形ABC经过某种变换得到的图形，点A与点D，点B与点E，点C与点F分别是对应点，观察点与点的坐标之间的关系，解答下列问题：
(1)分别写出点A与点D，点B与点E，点C与点F的坐标，并说说对应点的坐标有哪些特征；
(2)若点P(a＋3，4－b)与点Q(2a，2b－3)也是通过上述变换得到的对应点，求a，b的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了节约用水，某市决定调整居民用水收费方法，规定如果每户每月用水不超过10吨，每吨水收费2元，如果每户每月用水超过10吨，则超过部分每吨水收费2.5元；小红看到这种收费方法后，想算算她家每月的水费：
（1）如果小红家每月用水8吨，则水费是 元；如果小红家每月用水20吨，则水费是 元．
（2）如果字母
表示小红家每月用水的吨数，那么小红家每月的水费该如何用
的代数式表示呢？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com