
����Ŀ���ڵ�����ABC�У�
��1����ͼ1������ABCΪ�ȱ������Σ�DΪ�߶�BC�е㣬�߶�AD����ֱ��AB�ĶԳ��߶�Ϊ�߶�AE������DE�����BDE�Ķ���Ϊ___________��
��2������ABCΪ�ȱ������Σ���DΪ�߶�BC��һ���㣨����B��C�غϣ�������AD�����߶�AD�Ƶ�D��ʱ����ת60���õ��߶�DE������BE.
�ٸ���������ͼ2�в�ȫͼ�Σ�
��С��ͨ���۲졢��֤������²⣺�ڵ�D�˶��Ĺ����У�����CD=BE.������ͬѧ�ǵij�����ۣ��γ��˼���֤����˼·��
˼·1��Ҫ֤��CD=BE��ֻ��Ҫ����AE����֤����ADC�ա�AEB��
˼·2��Ҫ֤��CD=BE��ֻ��Ҫ����D��DF��AB����AC��F��֤����ADF�ա�DEB��
˼·3��Ҫ֤��CD=BE��ֻ��Ҫ�ӳ�CB����G��ʹ��BG=CD��֤����ADC�ա�DEG��
����
��ο�����˼·������С��֤��CD=BE.��ֻ��Ҫ��һ�ַ���֤�����ɣ�
��3��С��ķ���������С������ͼ3����AB=AC=kBC��AD=kDE���ҡ�ADE=��C����ʱС������BE��BD��AC����֮������һ���ĵ�������ϵ�����������ϵ��______________________.��ֱ�Ӹ�����������֤����
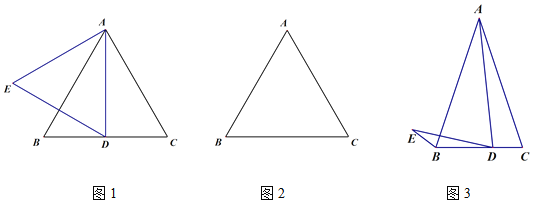
���𰸡���1��30�㣻��2���𰸼���������3��k(BE+BD)=AC
�������������������1����AD�ǵȱ�������ABC��BC���ϵ����ߵ�AD��BC����AE��AD����AB�Գƣ��Ӷ�AB��ֱƽ��DE���ɵ���ADE��60�㣬������BDE=30����
��2���ٸ������⻭ͼ���ɣ�
����˼·1��֤����EAB�ա�DAC���ɵó�����.
��3��k(BE+BD)=AC.
�����������1���ߦ�ABC�ǵȱ������Σ�D��BC�ߵ��е�
���BAD=30��
���߶�AD��AE����ֱ��AB�Գ�
��DE��AB
���ADE=60��
����BDE=90��-60��=30����
��2����ͼ���£�
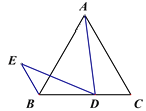
����ͼ������AE.
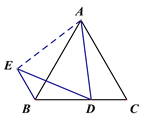
![]()
![]()
![]()
![]()
![]()
![]()
��3��k(BE+BD)=AC.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
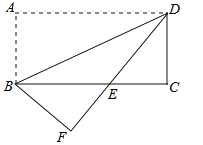
����Ŀ����ͼ��������ֽƬABCD�ضԽ���BD�۵���ʹ��A����ƽ���ϵ�F�㴦��DF��BC�ڵ�E��
��1����֤����DCE�ա�BFE��
��2����CD=2����ADB=30�㣬��BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ2018��12�³�������ȫʡ��Χ�ڵ�ǿ����,�����������5���Ϊ+5��,��-8���ʾ�� ��
A. �½�3�� B. ����3�� C. �½�8�� D. ����8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����ABC���DEC���ڵ�C�����ĶԳƣ�����AE��BD��
��1���߶�AE��BD����������λ�ù�ϵ�ʹ�С��ϵ��˵��������ɣ�
��2�������ABC�����Ϊ5cm2 �� ���ı���ABDE�������
��3������ACBΪ���ٶ�ʱ���ı���ABDEΪ���Σ�˵��������ɣ�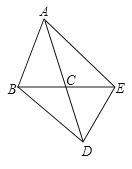
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABC�ƶ���B��ʱ�뷽����ת���ȵ���A1B1C1��λ�ã�AB��A1C1�ཻ�ڵ�D��AC��A1C1��BC1�ֱ��ڵ�E��F��
��1����֤����BCF�ա�BA1D��
��2������C=����ʱ���ж��ı���A1BCE����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������AB��BC��CD��DE��EA��ɵ�ƽ��ͼ�Σ����1+��2+��3+��4+��5= �� 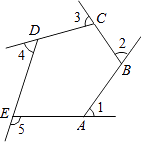
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�⣺��ͼ�������������е�ÿ��С�����εı߳�����1��ÿ��С�����εĶ��������㣮��AOB����������A��O��B���ڸ���ϣ�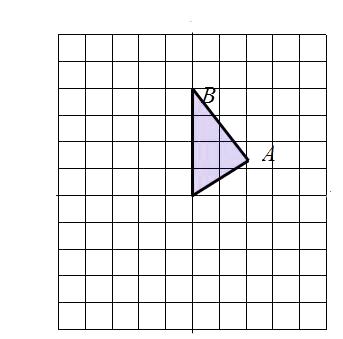
��1��������AOB���ڵ�O�����ĶԳƵ������Σ�
��2��������AOB�Ƶ�O��ʱ����ת90��õ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ˮ�շ�ʵ�н���ˮ�ۣ��շѱ����±���ʾ��
��1��ij�û����·���ˮ��Ϊ16�֣��轻ˮ��Ϊ����Ԫ��
��2��ij�û����·ݽ�ˮ��50Ԫ������ˮ��Ϊ���ٶ֣�
��3��ij�û����·���ˮ��Ϊa�֣���Ҫ��ˮ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com