
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α度时,判定四边形A1BCE的形状,并说明理由.

【答案】(1)证明见解析;(2)四边形A1BCE是菱形.
【解析】
试题分析:(1)根据等腰三角形的性质得到AB=BC,∠A=∠C,由旋转的性质得到A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,根据全等三角形的判定定理得到△BCF≌△BA1D;
(2)由旋转的性质得到∠A1=∠A,根据平角的定义得到∠DEC=180°﹣α,根据四边形的内角和得到∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,证得四边形A1BCE是平行四边形,由于A1B=BC,即可得到四边形A1BCE是菱形.
试题解析:(1)证明:∵△ABC是等腰三角形,∴AB=BC,∠A=∠C,∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,∴A1B=AB=BC,∠A=∠A1=∠C,∠A1BD=∠CBC1,在△BCF与△BA1D中,∵∠A1=∠C,A1B=BC,∠A1BD=∠CBF,∴△BCF≌△BA1D;
(2)解:四边形A1BCE是菱形,∵将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,∴∠A1=∠A,∵∠ADE=∠A1DB,∴∠AED=∠A1BD=α,∴∠DEC=180°﹣α,∵∠C=α,∴∠A1=α,∴∠ABC=360°﹣∠A1﹣∠C﹣∠A1EC=180°﹣α,∴∠A1=∠C,∠A1BC=∠AEC,∴四边形A1BCE是平行四边形,∴A1B=BC,∴四边形A1BCE是菱形.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
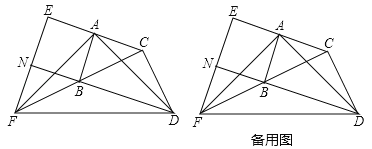
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.
(1)用含a的式子表示点B的坐标;
(2)经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,
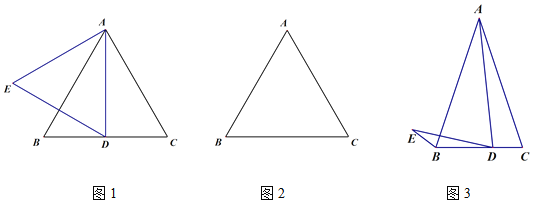
(1)如图1,若△ABC为等边三角形,D为线段BC中点,线段AD关于直线AB的对称线段为线段AE,连接DE,则∠BDE的度数为___________;
(2)若△ABC为等边三角形,点D为线段BC上一动点(不与B,C重合),连接AD并将线段AD绕点D逆时针旋转60°得到线段DE,连接BE.
①根据题意在图2中补全图形;
②小玉通过观察、验证,提出猜测:在点D运动的过程中,恒有CD=BE.经过与同学们的充分讨论,形成了几种证明的思路:
思路1:要证明CD=BE,只需要连接AE,并证明△ADC≌△AEB;
思路2:要证明CD=BE,只需要过点D作DF∥AB,交AC于F,证明△ADF≌△DEB;
思路3:要证明CD=BE,只需要延长CB至点G,使得BG=CD,证明△ADC≌△DEG;
……
请参考以上思路,帮助小玉证明CD=BE.(只需要用一种方法证明即可)
(3)小玉的发现启发了小明:如图3,若AB=AC=kBC,AD=kDE,且∠ADE=∠C,此时小明发现BE,BD,AC三者之间满足一定的的数量关系,这个数量关系是______________________.(直接给出结论无须证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
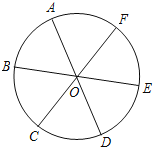
【题目】如图,点A、B、C、D、E、F为⊙O的六等分点,动点P从圆心O出发,沿OE弧EFFO的路线做匀速运动,设运动的时间为t,∠BPD的度数为y,则下列图象中表示y与t之间函数关系最恰当的是( )
A.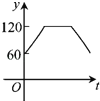 B.
B.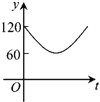 C.
C.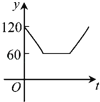 D.
D.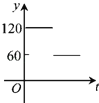
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若点P(a,b)在函数y=![]() 的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的图象上,将以a为二次项系数,b为一次项系数构造的二次函数y=ax2+bx称为函数y=![]() 的一个“派生函数”.例如:点(2,
的一个“派生函数”.例如:点(2, ![]() )在函数y=
)在函数y=![]() 的图象上,则函数y=2x2+
的图象上,则函数y=2x2+ ![]() 称为函数y=
称为函数y=![]() 的一个“派生函数”.现给出以下两个命题:
的一个“派生函数”.现给出以下两个命题:
(1)存在函数y=![]() 的一个“派生函数”,其图象的对称轴在y轴的右侧
的一个“派生函数”,其图象的对称轴在y轴的右侧
(2)函数y=![]() 的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
的所有“派生函数”的图象都经过同一点,下列判断正确的是( )
A. 命题(1)与命题(2)都是真命题
B. 命题(1)与命题(2)都是假命题
C. 命题(1)是假命题,命题(2)是真命题
D. 命题(1)是真命题,命题(2)是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com