
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.
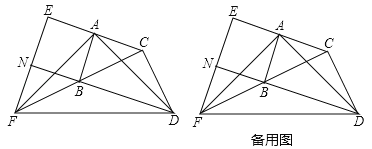
(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)四边形ABNE是正方形.
【解析】
试题分析:(1)由等腰直角三角形的性质得出∠ABC=∠ACB=45°,求出∠ABF=135°,∠ABF=∠ACD,证出BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;
(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;
(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
试题解析:(1)∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,∴∠ABF=135°,∵∠BCD=90°,∴∠ABF=∠ACD,∵CB=CD,CB=BF,∴BF=CD,在△ABF和△ACD中,∵AB=AC,∠ABF=∠ACD,BF=CD,∴△ABF≌△ACD(SAS),∴AD=AF;
(2)由(1)知,AF=AD,△ABF≌△ACD,∴∠FAB=∠DAC,∵∠BAC=90°,∴∠EAB=∠BAC=90°,∴∠EAF=∠BAD,在△AEF和△ABD中,∵AE=AB,∠EAF=∠BAD,AF=AD,∴△AEF≌△ABD(SAS),∴BD=EF;
(3)四边形ABNE是正方形;理由如下:
∵CD=CB,∠BCD=90°,∴∠CBD=45°,由(2)知,∠EAB=90°,△AEF≌△ABD,∴∠AEF=∠ABD=90°,∴四边形ABNE是矩形,又∵AE=AB,∴四边形ABNE是正方形.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】湖北省2018年12月初出现了全省范围内的强降温,如果气温上升5℃记为+5℃,则-8℃表示( )
A. 下降3℃ B. 上升3℃ C. 下降8℃ D. 上升8℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() ,其中
,其中![]() .
.
(1)求该二次函数的对称轴方程;
(2)过动点C(0, ![]() )作直线
)作直线![]() ⊥y轴.
⊥y轴.
① 当直线![]() 与抛物线只有一个公共点时, 求
与抛物线只有一个公共点时, 求![]() 与
与![]() 的函数关系;
的函数关系;
② 若抛物线与x轴有两个交点,将抛物线在![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折,图象的其余部分保持不变,得到一个新的图象. 当
轴翻折,图象的其余部分保持不变,得到一个新的图象. 当![]() =7时,直线
=7时,直线![]() 与新的图象恰好有三个公共点,求此时
与新的图象恰好有三个公共点,求此时![]() 的值;
的值;
(3)若对于每一个给定的x的值,它所对应的函数值都不小于1,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ABC与△DEC关于点C成中心对称,连接AE、BD.
(1)线段AE、BD具有怎样的位置关系和大小关系?说明你的理由.
(2)如果△ABC的面积为5cm2 , 求四边形ABDE的面积.
(3)当∠ACB为多少度时,四边形ABDE为矩形?说明你的理由.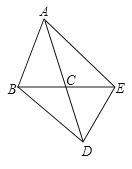
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.
(1)求证:△BCF≌△BA1D;
(2)当∠C=α度时,判定四边形A1BCE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△AOB的三个顶点A,O,B都在格点上.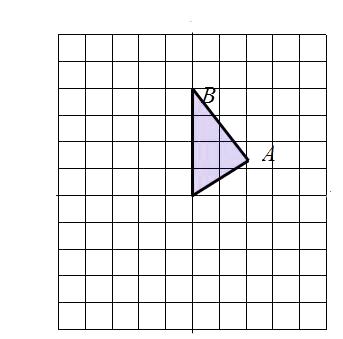
(1)画出△AOB关于点O成中心对称的三角形;
(2)画出△AOB绕点O逆时针旋转90后得到的三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com