【题目】已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．
（1）求证：BD=CE；
（2）求证：∠M=∠N．
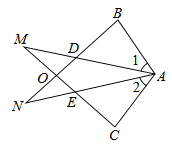
【答案】（1）答案见解析；（2）答案见解析．
【解析】
试题分析：（1）由SAS证明△ABD≌△ACE，得出对应边相等即可
（2）证出∠BAN=∠CAM，由全等三角形的性质得出∠B=∠C，由AAS证明△ACM≌△ABN，得出对应角相等即可．
试题解析：（1）在△ABD和△ACE中，∵AB=AC，∠1=∠2，AD=AE，∴△ABD≌△ACE（SAS），∴BD=CE；
（2）∵∠1=∠2，∴∠1+∠DAE=∠2+∠DAE，即∠BAN=∠CAM，由（1）得：△ABD≌△ACE，∴∠B=∠C，在△ACM和△ABN中，∵∠C=∠BA，AC=AB，∠CAM=∠CAN，∴△ACM≌△ABN（ASA），∴∠M=∠N．
科目：初中数学 来源： 题型：
【题目】设平面内一点到等边三角形中心的距离为d，等边三角形的内切圆半径为r，外接圆半径为R .对于一个点与等边三角形，给出如下定义：满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中，等边△ABC的三个顶点的坐标分别为A(0，2)，B（﹣
，﹣1），C(
，﹣1).
（1）已知点D（2，2），E（
，1），F（
，﹣1）.在D，E，F中，是等边△ABC的中心关联点的是 ；
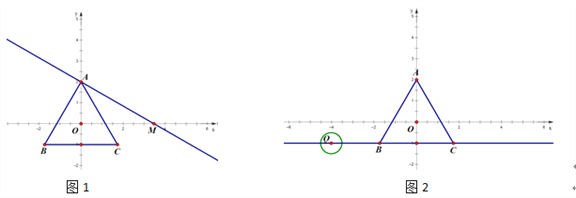
（2）如图1，过点A作直线交x轴正半轴于M，使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P（m，n），求m的取值范围；
②将直线AM向下平移得到直线y=kx+b，当b满足什么条件时，直线y=kx+b上总存在等边△ABC的中心关联点；（直接写出答案，不需过程）
（3）如图2，点Q为直线y=﹣1上一动点，⊙Q的半径为
.当Q从点（﹣4，﹣1）出发，以每秒1个单位的速度向右移动，运动时间为t秒.是否存在某一时刻t，使得⊙Q上所有点都是等边△ABC的中心关联点？如果存在，请直接写出所有符合题意的t的值；如果不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店需要购进甲、乙两种商品共180件，其进价和售价如表：（注：获利=售价﹣进价）
甲 | 乙 | |
进价（元/件） | 14 | 35 |
售价（元/件） | 20 | 43 |
（1）若商店计划销售完这批商品后能获利1240元，问甲、乙两种商品应分别购进多少件？
（2）若商店计划投入资金少于5040元，且销售完这批商品后获利多于1312元，请问有哪几种购货方案？并直接写出其中获利最大的购货方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下面的证明． 已知：如图，BE∥CD，∠A=∠1，
求证：∠C=∠E．
证明：∵BE∥CD （已知 ）
∴∠2=∠C （）
又∵∠A=∠1 （已知 ）
∴AC∥DE （）
∴∠2=∠E （）
∴∠C=∠E （等量代换 ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC和△BCD中，∠BAC=∠BCD=90°，AB=AC，CB=CD．延长CA至点E，使AE=AC；延长CB至点F，使BF=BC．连接AD，AF，DF，EF．延长DB交EF于点N．
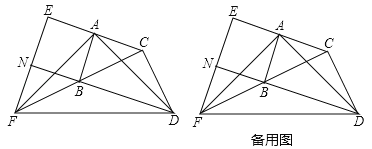
（1）求证：AD=AF；
（2）求证：BD=EF；
（3）试判断四边形ABNE的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：若点P（a，b）在函数y=
的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的一个“派生函数”．例如：点（2， 
）在函数y=
的图象上，则函数y=2x2+ 
称为函数y=
的一个“派生函数”．现给出以下两个命题：
（1）存在函数y=
的一个“派生函数”，其图象的对称轴在y轴的右侧
（2）函数y=
的所有“派生函数”的图象都经过同一点，下列判断正确的是（ ）
A. 命题（1）与命题（2）都是真命题
B. 命题（1）与命题（2）都是假命题
C. 命题（1）是假命题，命题（2）是真命题
D. 命题（1）是真命题，命题（2）是假命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
