【题目】若关于x的方程（a+3）x|a|﹣1﹣3x+2=0是一元二次方程，则a的值为 ．
科目：初中数学 来源： 题型：
【题目】完成下面的证明． 已知：如图，BE∥CD，∠A=∠1，
求证：∠C=∠E．
证明：∵BE∥CD （已知 ）
∴∠2=∠C （）
又∵∠A=∠1 （已知 ）
∴AC∥DE （）
∴∠2=∠E （）
∴∠C=∠E （等量代换 ）
查看答案和解析>>
科目：初中数学 来源： 题型：
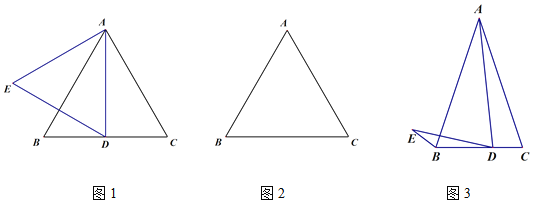
【题目】在等腰△ABC中，
（1）如图1，若△ABC为等边三角形，D为线段BC中点，线段AD关于直线AB的对称线段为线段AE，连接DE，则∠BDE的度数为___________；
（2）若△ABC为等边三角形，点D为线段BC上一动点（不与B，C重合），连接AD并将线段AD绕点D逆时针旋转60°得到线段DE，连接BE.
①根据题意在图2中补全图形；
②小玉通过观察、验证，提出猜测：在点D运动的过程中，恒有CD=BE.经过与同学们的充分讨论，形成了几种证明的思路：
思路1：要证明CD=BE，只需要连接AE，并证明△ADC≌△AEB；
思路2：要证明CD=BE，只需要过点D作DF∥AB，交AC于F，证明△ADF≌△DEB；
思路3：要证明CD=BE，只需要延长CB至点G，使得BG=CD，证明△ADC≌△DEG；
……
请参考以上思路，帮助小玉证明CD=BE.（只需要用一种方法证明即可）
（3）小玉的发现启发了小明：如图3，若AB=AC=kBC，AD=kDE，且∠ADE=∠C，此时小明发现BE，BD，AC三者之间满足一定的的数量关系，这个数量关系是______________________.（直接给出结论无须证明）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：
①AC=AD；②BD⊥AC；③四边形ACED是菱形．
其中正确的个数是（ ）
A．0 B．1 C．2 D．3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：若点P（a，b）在函数y=
的图象上，将以a为二次项系数，b为一次项系数构造的二次函数y=ax2+bx称为函数y=
的一个“派生函数”．例如：点（2， 
）在函数y=
的图象上，则函数y=2x2+ 
称为函数y=
的一个“派生函数”．现给出以下两个命题：
（1）存在函数y=
的一个“派生函数”，其图象的对称轴在y轴的右侧
（2）函数y=
的所有“派生函数”的图象都经过同一点，下列判断正确的是（ ）
A. 命题（1）与命题（2）都是真命题
B. 命题（1）与命题（2）都是假命题
C. 命题（1）是假命题，命题（2）是真命题
D. 命题（1）是真命题，命题（2）是假命题
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在同一平面内，将△ABC绕点A旋转到△AED的位置，若AE⊥BC，∠ADC=65°，则∠ABC的度数为（ ）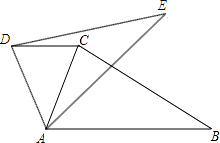
A.30°
B.40°
C.50°
D.60°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1（A、B分别对应A1、B1），则直线AB与直线A1B1的夹角（锐角）为（ ）
A.130°
B.50°
C.40°
D.60°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
